题目内容
 如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.
如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.考点:切线的判定,角平分线的性质
专题:
分析:利用切线的性质得出PD⊥OA,再利用全等三角形的判定方法得出△OPE≌△OPD(AAS),进而得出答案.
解答: 解:⊙P与OB相切,
解:⊙P与OB相切,
理由:设OA与⊙P相切于点D,过点P作PE⊥OB于点E,
∵OA与⊙P相切于点D,
∴PD⊥OA,
在△OPE和△OPD中,
,
∴△OPE≌△OPD(AAS),
∴PE=PD,
∴⊙P与OB相切.
 解:⊙P与OB相切,
解:⊙P与OB相切,理由:设OA与⊙P相切于点D,过点P作PE⊥OB于点E,
∵OA与⊙P相切于点D,
∴PD⊥OA,
在△OPE和△OPD中,
|
∴△OPE≌△OPD(AAS),
∴PE=PD,
∴⊙P与OB相切.
点评:此题主要考查了切线的判定与性质以及全等三角形的判定与性质等知识,得出△OPE≌△OPD是解题关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
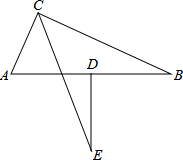 在△ABC中,已知AB=13,BC=12,CA=5,D为边AB的中点,DE⊥AB且与∠ACB的平分线交于点E,求DE的长.
在△ABC中,已知AB=13,BC=12,CA=5,D为边AB的中点,DE⊥AB且与∠ACB的平分线交于点E,求DE的长.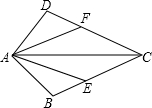 已知,如图,AB=AD,CE=CF,AC是∠DAB的平分线,求证:AE=AF.
已知,如图,AB=AD,CE=CF,AC是∠DAB的平分线,求证:AE=AF.