题目内容
14.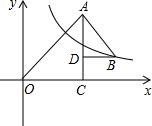 如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )
如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )| A. | 12 | B. | 9 | C. | 8 | D. | 6 |
分析 设B点坐标为(a,b),根据等腰直角三角形的性质得OA=$\sqrt{2}$AC,AB=$\sqrt{2}$AD,OC=AC,AD=BD,则OA2-AB2=18变形为AC2-AD2=9,利用平方差公式得到(AC+AD)(AC-AD)=9,所以(OC+BD)•CD=9,则有a•b=9,根据反比例函数图象上点的坐标特征易得k=9.
解答 解:设B点坐标为(a,b),
∵△OAC和△BAD都是等腰直角三角形,
∴OA=$\sqrt{2}$AC,AB=$\sqrt{2}$AD,OC=AC,AD=BD,
∵OA2-AB2=18,
∴2AC2-2AD2=18,即AC2-AD2=9,
∴(AC+AD)(AC-AD)=9,
∴(OC+BD)•CD=9,
∴a•b=9,
∴k=9.
故选:B.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
2.把多项式x3-4x分解因式,结果正确的是( )
| A. | x(x+2)(x-2) | B. | x(x+4)(x-4) | C. | x(x-2)2 | D. | x (x2-4) |
19.某超市四月份的营业额为30万元,第二季度的营业额为120万元,如果设平均每月的增长率为x,下列方程正确的是( )
| A. | 30(1+x)2=120 | B. | 30+30×2x=120 | ||
| C. | 30(1+x%)2=120 | D. | 30+30(1+x)+30(1+x)2=120 |
4.甲:在我是你今年的岁数时,你那年5岁.乙:在我是你今年的岁数时,你那年20岁.设甲、乙现在分别是x,y岁,则可列二元一次方程组为( )
| A. | $\left\{\begin{array}{l}{x-y=5}\\{x+y=20}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-(x-y)=5}\\{x+(x-y)=20}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-(x-y)=5}\\{y+(x-y)=20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y-(x-y)=10}\\{x+(x-y)=25}\end{array}\right.$ |
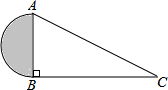 如图,∠ABC=90°,CB=15,AC=17,则阴影部分面积是多少?
如图,∠ABC=90°,CB=15,AC=17,则阴影部分面积是多少?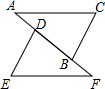 如图,已知AD=FB,AC∥EF,∠C=∠E,点A,D,B,F在一条直线上.请判定AC与EF的大小关系,并证明你的结论.
如图,已知AD=FB,AC∥EF,∠C=∠E,点A,D,B,F在一条直线上.请判定AC与EF的大小关系,并证明你的结论.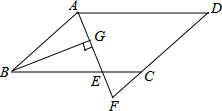 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=$4\sqrt{2}$,则△CEF的面积是2$\sqrt{2}$.
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=$4\sqrt{2}$,则△CEF的面积是2$\sqrt{2}$.