题目内容
5.k取何值时,直线x+2y+k+1=0,2x+y+2k=0的交点在第三象限内.分析 根据两直线相交的问题,通过解方程组$\left\{\begin{array}{l}{x+2y+k+1=0}\\{2x+y+2k=0}\end{array}\right.$得两直线的交点坐标,再利用第三象限内点的坐标特征得到以$\frac{1}{3}$-k<0,然后解不等式即可.
解答 解:解方程组$\left\{\begin{array}{l}{x+2y+k+1=0}\\{2x+y+2k=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{3}-k}\\{y=-\frac{2}{3}}\end{array}\right.$,
则两直线的交点坐标为($\frac{1}{3}$-k,-$\frac{2}{3}$),
因为点($\frac{1}{3}$-k,-$\frac{2}{3}$)在第三象限,
所以$\frac{1}{3}$-k<0,
解得k>$\frac{1}{3}$,
即k的取值范围为k>$\frac{1}{3}$.
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
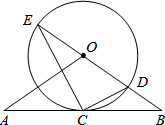 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.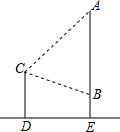 如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)
如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)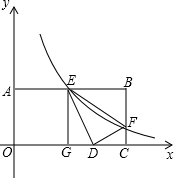 如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$.
如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$. 如图,已知∠AED=∠C,DE交AB于D,交AC于E,则∠1=∠2吗?请说明理由.
如图,已知∠AED=∠C,DE交AB于D,交AC于E,则∠1=∠2吗?请说明理由. 如图,已知△ABC,点D,过点D作△ABC平移后的图形△DEF,使点A移动到点D.(其中点B与点E是对应点,点C与点F是对应点)
如图,已知△ABC,点D,过点D作△ABC平移后的图形△DEF,使点A移动到点D.(其中点B与点E是对应点,点C与点F是对应点)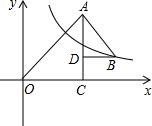 如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )
如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )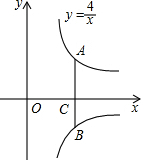 已知函数y=$\frac{4}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象如图所示,点C在x轴正半轴上一点,过点C作AB∥y轴分别交两个图象于点A、B,若AC=2BC,则k=-2.
已知函数y=$\frac{4}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象如图所示,点C在x轴正半轴上一点,过点C作AB∥y轴分别交两个图象于点A、B,若AC=2BC,则k=-2.