题目内容
4．
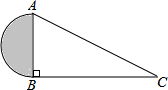如图，∠ABC=90°，CB=15，AC=17，则阴影部分面积是多少？
分析 在直角三角形ABC中，由CB与AC的长，利用勾股定理求出AB的长，即为半圆的直径，求出半圆面积即为阴影部分面积．
解答 解：在Rt△ABC中，CB=15，AC=17，
根据勾股定理得：AB=$\sqrt{A{C}^{2}-C{B}^{2}}$=8，
则S阴影=$\frac{1}{2}$π（$\frac{AB}{2}$）2=8π．
点评 此题考查了勾股定理，以及圆的面积求法，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
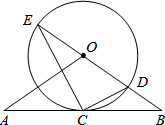如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，D，连接EC，CD．
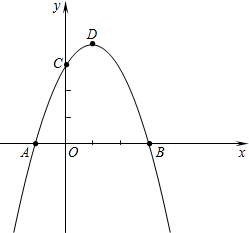如图，在平面直角坐标系中，二次函数y=ax2+bx+c（a≠0）的图象经过点A（-1，0）、点B（3，0）、点C（0，3）．
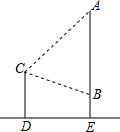如图所示，小明、小军、小丽三个同学家正好住在一个小区，小军和小丽家在同一栋楼AE里，高度相差AB为（42+14$\sqrt{3}$）米，小明家在他们相对的一栋楼CD上，一日，小明站在自家阳台C处，发现小军家住A处，且仰角为45°，而小丽家在B处，俯角为30°，小丽家离地面高度BE=6米，试求两栋楼之间的距离DE及小明家离地面的高度CD（$\sqrt{3}$=1.73，结果精确到0.01）
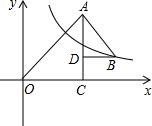如图所示，OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B，若OA2-AB2=18，则k的值为（ ）