题目内容
9.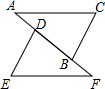 如图,已知AD=FB,AC∥EF,∠C=∠E,点A,D,B,F在一条直线上.请判定AC与EF的大小关系,并证明你的结论.
如图,已知AD=FB,AC∥EF,∠C=∠E,点A,D,B,F在一条直线上.请判定AC与EF的大小关系,并证明你的结论.
分析 求出AB=DF,根据平行线性质求出∠A=∠E,根据AAS推出△ABC≌△FDE即可.
解答 AC=EF,
证明:∵AD=BF,
∴AD+DB=BF+DB,
∴AB=DF,
∵AC∥EF,
∴∠A=∠E,
在△ABC和△FDE中
$\left\{\begin{array}{l}{∠A=∠F}\\{∠C=∠E}\\{AB=DF}\end{array}\right.$
∴△ABC≌△FDE(AAS),
∴AC=EF.
点评 本题考查了全等三角形的性质和判定,平行线的性质的应用,解此题的关键是推出△ABC≌△FDE,注意:全等三角形的对应边相等,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.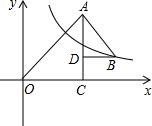 如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )
如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )
 如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )
如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )| A. | 12 | B. | 9 | C. | 8 | D. | 6 |
18.已知菱形的一个内角为120°,且平分这个内角的对角线长为9cm,则这个菱形的周长为( )
| A. | 18 | B. | 72 | C. | 36 | D. | 54 |
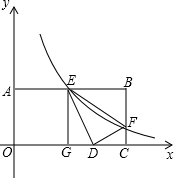 如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$.
如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$. 如图,已知△ABC,点D,过点D作△ABC平移后的图形△DEF,使点A移动到点D.(其中点B与点E是对应点,点C与点F是对应点)
如图,已知△ABC,点D,过点D作△ABC平移后的图形△DEF,使点A移动到点D.(其中点B与点E是对应点,点C与点F是对应点)
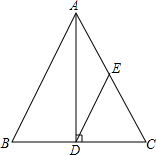 如图,在△ABC中,AB=AC,AD⊥BC于点D,E是AC的中点,BC=4,AD=4$\sqrt{2}$,求DE的长.
如图,在△ABC中,AB=AC,AD⊥BC于点D,E是AC的中点,BC=4,AD=4$\sqrt{2}$,求DE的长.