题目内容
12.若x,y都是实数,且满足(x2+y2)(x2+y2-1)=12,则x2+y2的值为4.分析 设x2+y2=t,原方程变形为t(t-1)=12,解得t,再根据x2+y2>0,即可得出答案.
解答 解:设x2+y2=t,
原方程变形为t(t-1)=12,
t2-t=12
(t-4)(t+3)=0,
t1=4,t2=-3,
∵x2+y2>0,
∴t=4
∴x2+y2=4,
故答案为4.
点评 本题考查了用换元法解一元二次方程,掌握换元的整体x2+y2=t是解题的关键.

练习册系列答案
相关题目
7.当m,n是实数且满足m-n=mn时,就称点Q(m,$\frac{m}{n}}$)为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y=$\frac{2}{x}$的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
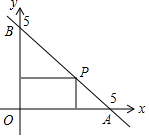 如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )
如图,一次函数的图象与两坐标轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是( )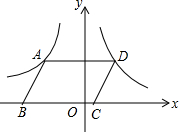 如图,在平面直角坐标系中,?ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=-$\frac{3}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象上,则?ABCD的面积为4.
如图,在平面直角坐标系中,?ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=-$\frac{3}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象上,则?ABCD的面积为4.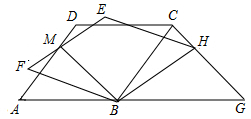 如图,菱形ABCD边长为5,tan∠DAB=$\frac{4}{3}$,将菱形绕点B按顺时针方向旋转角α(0°<α<∠DBA)得到菱形FBHE(点A的对应点为点F),EF与AD交于点M,连接BM.
如图,菱形ABCD边长为5,tan∠DAB=$\frac{4}{3}$,将菱形绕点B按顺时针方向旋转角α(0°<α<∠DBA)得到菱形FBHE(点A的对应点为点F),EF与AD交于点M,连接BM.