Question

13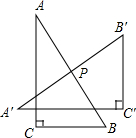．如图，将Rt△ABC绕斜边AB的中点P旋转到△A′B′C′的位置，使得A′C′∥BC，则旋转角等于（　　）

• A． 60°
• B． 80°
• C． 90°
• D． 100°

Answer 1

分析 先根据旋转的性质得∠A=∠A′，∠APA′等于旋转角，再利用平行线的性质得到∠1=∠B，然后利用∠A+∠B=90°得到∠1+∠A′=90°，则∠APA′=90°，于是得到旋转角的度数．

解答 解：∵Rt△ABC绕斜边AB的中点P旋转到△A′B′C′的位置，
∴∠A=∠A′，∠APA′等于旋转角，
∵A′C′∥BC，
∴∠1=∠B，
而∠A+∠B=90°，
∴∠1+∠A′=90°，
∴∠APA′=∠A′+∠1=90°，
即旋转角等于90°．
故选C．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．