题目内容
已知,AB∥CD,点M、N分别在AB、CD上,点P是一个动点,连接MP、NP.
(1)当动点P落在图1位置时,请探讨∠P与∠AMP、∠CNP之间的关系,并说明理由;
(2)当动点P落在图2位置时,请探讨∠P与∠AMP、∠CNP之间的关系,并说明理由;
(3)当动点P落在图3位置时,请探讨∠P与∠AMP、∠CNP之间的关系.(直接写出答案,不需要说明理由)
(4)当动点P落在图4位置时,请探讨∠P与∠AMP、∠CNP之间的关系.(直接写出答案,不需要说明理由)

(1)当动点P落在图1位置时,请探讨∠P与∠AMP、∠CNP之间的关系,并说明理由;
(2)当动点P落在图2位置时,请探讨∠P与∠AMP、∠CNP之间的关系,并说明理由;
(3)当动点P落在图3位置时,请探讨∠P与∠AMP、∠CNP之间的关系.(直接写出答案,不需要说明理由)
(4)当动点P落在图4位置时,请探讨∠P与∠AMP、∠CNP之间的关系.(直接写出答案,不需要说明理由)
考点:平行线的性质
专题:
分析:(1)过点P作PQ∥AB,根据平行公理可得PQ∥CD,再根据两直线平行,内错角相等可得∠AMP=∠1,∠CNP=∠2,然后根据∠P=∠1+∠2等量代换即可得解;
(2)过点P作PQ∥AB,根据平行公理可得PQ∥CD,再根据两直线平行,同旁内角互补可得∠AMP=180°-∠1,∠CNP=180°-∠2,然后根据∠P=∠1+∠2等量代换即可得解;
(3)(4)分别过点P作PQ∥AB,然后根据平行线的性质解答即可.
(2)过点P作PQ∥AB,根据平行公理可得PQ∥CD,再根据两直线平行,同旁内角互补可得∠AMP=180°-∠1,∠CNP=180°-∠2,然后根据∠P=∠1+∠2等量代换即可得解;
(3)(4)分别过点P作PQ∥AB,然后根据平行线的性质解答即可.
解答: 解:(1)如图1,过点P作PQ∥AB,
解:(1)如图1,过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=∠1,∠CNP=∠2,
∵∠P=∠1+∠2,
∴∠P=∠AMP+∠CNP;
(2)如图2,过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=180°-∠1,∠CNP=180°-∠2,
∴∠AMP+∠CNP=180°×2-∠1-∠2,
∵∠P=∠1+∠2,
∴∠P+∠AMP+∠CNP=360°;
(3)∠P=∠CNP-∠AMP;
(4)∠P=∠AMP-∠CNP.
 解:(1)如图1,过点P作PQ∥AB,
解:(1)如图1,过点P作PQ∥AB,∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=∠1,∠CNP=∠2,
∵∠P=∠1+∠2,
∴∠P=∠AMP+∠CNP;
(2)如图2,过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD∥AB,
∴∠AMP=180°-∠1,∠CNP=180°-∠2,
∴∠AMP+∠CNP=180°×2-∠1-∠2,
∵∠P=∠1+∠2,
∴∠P+∠AMP+∠CNP=360°;
(3)∠P=∠CNP-∠AMP;
(4)∠P=∠AMP-∠CNP.
点评:本题考查了平行线的性质,此类题目,关键在于过拐点作平行线.

练习册系列答案
相关题目
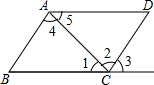 填空:
填空: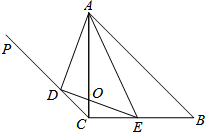 已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O. 已知:∠1+∠2=180°,∠B=∠3.求证:∠AFE=∠ACB.
已知:∠1+∠2=180°,∠B=∠3.求证:∠AFE=∠ACB.