题目内容
已知整数x、y、z两两互质，且x＜y＜z，其中任一个必整除另两个之和，求这三个数．
考点：整数问题的综合运用
专题：
分析：由x＜y＜z，得出x+y＜2z，再根据其中任一个必整除另两个之和，得出x+y=z，设y+z=nx．代入得出x+y+z=2z=（n+1）x，进一步分析探讨得出答案即可．
解答：解：∵x＜y＜z，
∴x+y＜2z，
∵其中任一个必整除另两个之和，
z如果要整除x+y，
∴只能x+y=z，
x整除（y+z），设y+z=nx．
∴x+y+z=2z=（n+1）x，
又∵x、z互质，
∴x=1或x=2，
同样有y=1或y=2
∴x=1，y=2，z=3．
∴x+y＜2z，
∵其中任一个必整除另两个之和，
z如果要整除x+y，
∴只能x+y=z，
x整除（y+z），设y+z=nx．
∴x+y+z=2z=（n+1）x，
又∵x、z互质，
∴x=1或x=2，
同样有y=1或y=2
∴x=1，y=2，z=3．
点评：此题考查整数的综合运用，注意整数的性质以及整除的性质探讨得出答案解．
练习册系列答案
相关题目
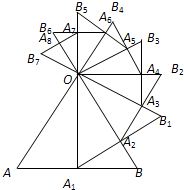如图，已知等边△OAB的边长为32，以AB边上的高OA1为边，按逆时针方向作等边△OA1B1，A1B1与OB相交于点A2，再以OA2为边按逆时针方向作等边△OA2B2，A2B2与OB1相交于点A3，按此作法进行下去，得到△OA3B3，△OA4B4，…，△OAnBn
一只蚂蚁从长为12cm、宽为3cm，高是4cm的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是
已知：如图，∠1=∠3，∠2=∠4，则△