题目内容
用适当的方法解一元二次方程:
(1)(6x-1)2=25;
(2)3x2-5x-2=0;
(3)x2+4x+3=0;
(4)(2x+1)2-3(2x+1)=0.
(1)(6x-1)2=25;
(2)3x2-5x-2=0;
(3)x2+4x+3=0;
(4)(2x+1)2-3(2x+1)=0.
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法
专题:计算题
分析:(1)方程利用平方根定义开方即可求出解;
(2)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(3)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(4)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(2)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(3)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(4)方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
解答:解:(1)开方得:6x-1=±5,
解得:x1=1,x2=-
;
(2)分解因式得:(3x+1)(x-2)=0,
可得3x+1=0或x-2=0,
解得:x1=-
,x2=2;
(3)分解因式得:(x+1)(x+3)=0,
可得x+1=0或x+3=0,
解得:x1=-1,x2=-3;
(4)分解因式得:(2x+1)(2x+1-3)=0,
可得2x+1=0或2x+1-3=0,
解得:x1=-
,x2=1.
解得:x1=1,x2=-
| 2 |
| 3 |
(2)分解因式得:(3x+1)(x-2)=0,
可得3x+1=0或x-2=0,
解得:x1=-
| 1 |
| 3 |
(3)分解因式得:(x+1)(x+3)=0,
可得x+1=0或x+3=0,
解得:x1=-1,x2=-3;
(4)分解因式得:(2x+1)(2x+1-3)=0,
可得2x+1=0或2x+1-3=0,
解得:x1=-
| 1 |
| 2 |
点评:此题考查了解一元二次方程-直接开平方法,以及因式分解法,熟练掌握各自解法是解本题的关键.

练习册系列答案
相关题目
某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A、36(1-x)2=36-25 |
| B、36(1-x)2=25 |
| C、36(1-2x)=25 |
| D、36(1-x2)=25 |

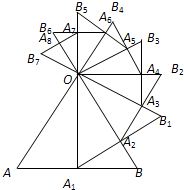 如图,已知等边△OAB的边长为32,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2,再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn
如图,已知等边△OAB的边长为32,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2,再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn 一只蚂蚁从长为12cm、宽为3cm,高是4cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是
一只蚂蚁从长为12cm、宽为3cm,高是4cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是