题目内容
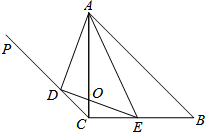 已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.(1)求证:△ADE∽△ACB;
(2)设CD=x,tan∠BAE=y,求y关于x的函数解析式,并写出它的定义域;
(3)如果△COD与△BEA相似,求CD的值.
考点:相似形综合题
专题:
分析:(1)首先利用两角对应相等,证明△ACD∽△ABE,进而证明△ADE∽△ACB;
(2)如答图1所示,过点D作DF⊥AC于点F,则△DCF为等腰直角三角形;分别求出CF、DF、AF的长度,然后利用tan∠BAE=tan∠CAD求解;
(3)首先确定△COD∽△BEA,然后证明AE为角平分线;如答图3,作辅助线,利用角平分线与等腰直角三角形的性质,求出CD的长度.
(2)如答图1所示,过点D作DF⊥AC于点F,则△DCF为等腰直角三角形;分别求出CF、DF、AF的长度,然后利用tan∠BAE=tan∠CAD求解;
(3)首先确定△COD∽△BEA,然后证明AE为角平分线;如答图3,作辅助线,利用角平分线与等腰直角三角形的性质,求出CD的长度.
解答:(1)证明:由题意可知∠CAD+∠CAE=∠CAE+∠BAE=45°,
∴∠CAD=∠BAE;
∵CP∥AB,∴∠ACD=∠CAE=∠B=45°.
∴△ACD∽△ABE,
∴
=
,即
=
,
又∵∠DAE=∠CAB=45°,
∴△ADE∽△ACB.
(2)解:∵等腰直角△ABC中,斜边AB的长为4,
∴AC=BC=2
.
如答图1,过点D作DF⊥AC于点F,则△DCF为等腰直角三角形,
∴DF=CF=
CD=
x,
∴AF=AC-CF=2
-
x,
∴tan∠CAD=
=
=
.
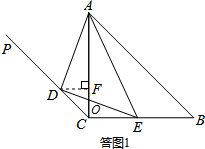
由(1)知,∠BAE=∠CAD,∴tan∠BAE=tan∠CAD,
∴y=
,定义域0<x<2.
(3)解:在△COD与△BEA中,∠DCO=∠B=45°,∠DOC与∠AEB均为钝角,
∴如果△COD与△BEA相似,只能是△COD∽△BEA,∴∠1=∠2.
∵∠AEC=∠AED+∠3=45°+∠3,∠AEC=∠B+∠2=45°+∠2,
∴∠3=∠2,
∴∠1=∠2=∠3,∴CE=CD.
∵CP∥AB,∴∠DCE+∠B=180°,∴∠DCE=180°-∠B=135°,
∴∠1=∠2=∠3=
(180°-∠DCE)=22.5°,
∴∠2=
∠CAB,即AE为角平分线.
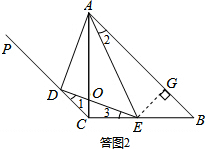
如答图2,过点E作EG⊥AB于点G,则EG=CE,且△BEG为等腰直角三角形.
∴EG=BG=CE=CD,BE=
EG=
CD.
∴BC=CE+BE=CD+
CD=2
,
∴CD=4-2
.
∴∠CAD=∠BAE;
∵CP∥AB,∴∠ACD=∠CAE=∠B=45°.
∴△ACD∽△ABE,
∴
| AD |
| AE |
| AC |
| AB |
| AD |
| AC |
| AE |
| AB |
又∵∠DAE=∠CAB=45°,
∴△ADE∽△ACB.
(2)解:∵等腰直角△ABC中,斜边AB的长为4,
∴AC=BC=2
| 2 |
如答图1,过点D作DF⊥AC于点F,则△DCF为等腰直角三角形,
∴DF=CF=
| ||
| 2 |
| ||
| 2 |
∴AF=AC-CF=2
| 2 |
| ||
| 2 |
∴tan∠CAD=
| DF |
| AF |
| ||||||
2
|
| x |
| 4-x |

由(1)知,∠BAE=∠CAD,∴tan∠BAE=tan∠CAD,
∴y=
| x |
| 4-x |
(3)解:在△COD与△BEA中,∠DCO=∠B=45°,∠DOC与∠AEB均为钝角,
∴如果△COD与△BEA相似,只能是△COD∽△BEA,∴∠1=∠2.
∵∠AEC=∠AED+∠3=45°+∠3,∠AEC=∠B+∠2=45°+∠2,
∴∠3=∠2,
∴∠1=∠2=∠3,∴CE=CD.
∵CP∥AB,∴∠DCE+∠B=180°,∴∠DCE=180°-∠B=135°,
∴∠1=∠2=∠3=
| 1 |
| 2 |
∴∠2=
| 1 |
| 2 |

如答图2,过点E作EG⊥AB于点G,则EG=CE,且△BEG为等腰直角三角形.
∴EG=BG=CE=CD,BE=
| 2 |
| 2 |
∴BC=CE+BE=CD+
| 2 |
| 2 |
∴CD=4-2
| 2 |
点评:本题是几何综合题,考查了等腰直角三角形、平行线、角平分线、相似三角形等几何知识点.本题着重考查几何基础知识,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固翼飞机的航空母舰,满载排水量为67500吨,这个数据67500用科学记数法表示为6.75×10n(n是正整数),则n的值等于
中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固翼飞机的航空母舰,满载排水量为67500吨,这个数据67500用科学记数法表示为6.75×10n(n是正整数),则n的值等于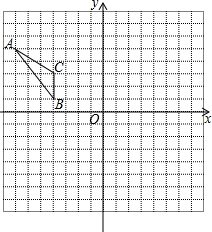 如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
