题目内容
解方程组:
.
|
考点:高次方程
专题:
分析:把第一个方程变形,得出两个方程,这样得出两个方程组,求出方程组的解即可.
解答:解:
,
由①得:(x-4y)(x+y)=0,
x-4y=0,x+y=0,
即原方程组变形为
,
,
解这两个方程组得:
,
.
即方程组的解为:
,
.
|
由①得:(x-4y)(x+y)=0,
x-4y=0,x+y=0,
即原方程组变形为
|
|
解这两个方程组得:
|
|
即方程组的解为:
|
|
点评:本题考查了解高次方程组的应用,解此题的关键是能把二元二次方程组转化成二元一次方程组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
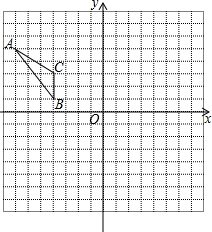 如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
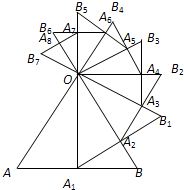 如图,已知等边△OAB的边长为32,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2,再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn
如图,已知等边△OAB的边长为32,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2,再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn
 如图,已知∠AOE=150°,且OE平分∠DOB,则∠AOC=
如图,已知∠AOE=150°,且OE平分∠DOB,则∠AOC=