题目内容
2.观察下列图形:
它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
| A. | 4+3(n-1) | B. | 4n | C. | 4n+1 | D. | 3n+4 |
分析 根据每个图形观察发现,每个图形上、左、右的五角星个数个图形序号一致,下方只有一个,根据规律即可求出答案.
解答 解:根据已知图形得:
第1个图形五角星个数:1×3+1,
第2个图形五角星个数:2×3+1,
第3个图形五角星个数:3×3+1,
第4个图形五角星个数:4×3+1,
由此规律得:
第2个图形五角星个数:n×3+1,
故第n个图形中共有3n+1个图形;
A答案为4+3(n-1)=3n+1.
故选A.
点评 题目考查了图形的变化类,属于规律型题目求解,通过图形的变化与图形序号的关系求出答案.题目整体较为简单,学生注意对A答案选项的化简,才能得出正确答案.

练习册系列答案
相关题目
13. 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )| A. | 0,1,-2 | B. | 1,0,-2 | C. | -2,0,1 | D. | 0,-2,1 |
 已知如图,AC、BD相交于点O,且被点O互相平分,求证:
已知如图,AC、BD相交于点O,且被点O互相平分,求证: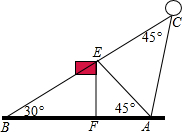 如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.
如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.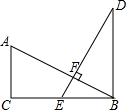 如图,已知AC⊥CB,DB⊥CB,AB⊥DE,垂足为F,AB=DE,E是BC的中点.
如图,已知AC⊥CB,DB⊥CB,AB⊥DE,垂足为F,AB=DE,E是BC的中点.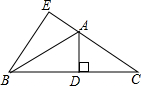 如图,在△ABC中,AB=AC,其中AD,BE都是△ABC的高.求证:∠BAD=∠CAD=∠EBC.
如图,在△ABC中,AB=AC,其中AD,BE都是△ABC的高.求证:∠BAD=∠CAD=∠EBC.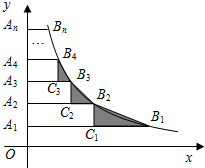 如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )
如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )