题目内容
12. 已知如图,AC、BD相交于点O,且被点O互相平分,求证:
已知如图,AC、BD相交于点O,且被点O互相平分,求证:(1)AB∥CD;
(2)AB=CD.
分析 (1)由SAS证明△AOB≌△COD,得出对应角相等∠OAB=∠OCD,即可得出结论;
(2)由全等三角形的对应边相等即可得出结论.
解答 证明:(1)∵AC、BD相交于点O,且被点O互相平分,
∴OA=OC,OB=OD,
在△AOB和△COD中,$\left\{\begin{array}{l}{OA=OC}&{\;}\\{∠AOB=∠COD}&{\;}\\{OB=OD}&{\;}\end{array}\right.$,
∴△AOB≌△COD(SAS),
∴∠OAB=∠OCD,
∴AB∥CD;
(2)由(1)得:△AOB≌△COD,
∴AB=CD.
点评 本题考查了全等三角形的判定与性质、平行线的判定;证明三角形全等是解决问题的关键,本题难度适中.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
2.观察下列图形:

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
| A. | 4+3(n-1) | B. | 4n | C. | 4n+1 | D. | 3n+4 |

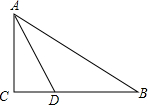 已知,在△ABC中,AD是角平分线,AD=BD,AB=2AC,求证:△ACB是直角三角形.
已知,在△ABC中,AD是角平分线,AD=BD,AB=2AC,求证:△ACB是直角三角形.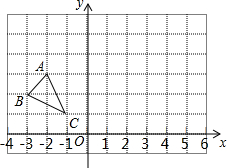 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.