题目内容
7.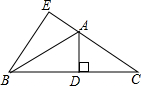 如图,在△ABC中,AB=AC,其中AD,BE都是△ABC的高.求证:∠BAD=∠CAD=∠EBC.
如图,在△ABC中,AB=AC,其中AD,BE都是△ABC的高.求证:∠BAD=∠CAD=∠EBC.
分析 先根据等腰三角形三线合一的性质得出∠BAD=∠CAD,再由三角形的高的定义得出∠BEC=∠ADC=90°,根据直角三角形两锐角互余得到∠EBC+∠C=90°,∠CAD+∠C=90°,根据同角的余角相等得出∠EBC=∠CAD,等量代换得到∠BAD=∠CAD=∠EBC.
解答 证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD.
∵BE⊥CE,AD⊥BC,
∴∠BEC=∠ADC=90°,
∴∠EBC+∠C=90°,∠CAD+∠C=90°,
∴∠EBC=∠CAD,
∴∠BAD=∠CAD=∠EBC.
点评 本题考查了等腰三角形三线合一的性质,三角形的高的定义,直角三角形的性质,余角的性质,证明出∠BAD=∠CAD,∠EBC=∠CAD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.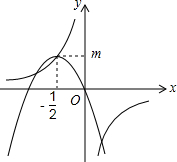 如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
 如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )| A. | a=b+2k | B. | a=b-2k | C. | k<b<0 | D. | a<k<0 |
2.观察下列图形:

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
| A. | 4+3(n-1) | B. | 4n | C. | 4n+1 | D. | 3n+4 |
12.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
