题目内容
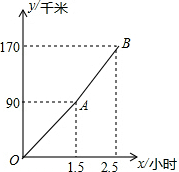“五一节”期间，申老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象（OA段和AB段）．（1）求他们出发半小时时，离家多少千米？
（2）他们出发2小时时，离目的地还有多少千米？
考点：一次函数的应用
专题：
分析：（1）设OA段图象的函数表达式为y=kx，然后利用待定系数法求一次函数解析式求出函数表达式，再把x=0.5代入计算即可得解；
（2）设AB段图象的函数表达式为y=mx+b，利用待定系数法求一次函数解析式求出函数表达式，再把x=2代入进行计算求出行驶的路程，再用全程减去行驶的路程计算即可得解．
（2）设AB段图象的函数表达式为y=mx+b，利用待定系数法求一次函数解析式求出函数表达式，再把x=2代入进行计算求出行驶的路程，再用全程减去行驶的路程计算即可得解．
解答：解：（1）设OA段图象的函数表达式为y=kx，
∵函数图象经过点A（1.5，90），
∴1.5k=90，
解得k=60，
∴y=60x（0≤x≤1.5），
当x=0.5时，y=60×0.5=30，
答：他们出发半小时时，离家30千米；
（2）设AB段图象的函数表达式为y=mx+b，
∵函数图象经过点A（1.5，90），B（2.5，170），
∴
，
解得
，
∴y=80x-30（1.5＜x≤2.5），
当x=2时，y=80×2-30=130，
∴170-130=40千米．
答：他们出发2小时时，离目的地还有40千米．
∵函数图象经过点A（1.5，90），
∴1.5k=90，
解得k=60，
∴y=60x（0≤x≤1.5），
当x=0.5时，y=60×0.5=30，
答：他们出发半小时时，离家30千米；
（2）设AB段图象的函数表达式为y=mx+b，
∵函数图象经过点A（1.5，90），B（2.5，170），
∴
|
解得
|
∴y=80x-30（1.5＜x≤2.5），
当x=2时，y=80×2-30=130，
∴170-130=40千米．
答：他们出发2小时时，离目的地还有40千米．
点评：本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式和函数值的求解，要注意（2）求的是离目的地的距离，这也是本题容易出错的地方．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
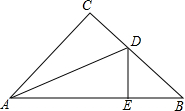如图，在△ABC中，∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB于E，若AC=m，CD=n，则△BDE的周长为（ ）| A、m+n | B、m-n |
| C、2m+n | D、2n+m |
一块铁板的形状如图，已知CA⊥AB，CB⊥BD，且AC=30cm，AB=40cm，BD=120cm．求CD的长度．
如图，已知四边形ABCD的顶点坐标分别为A（4，1），B（5，3），C（4，5），D（2，3）．