题目内容
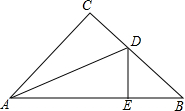 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=m,CD=n,则△BDE的周长为( )
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=m,CD=n,则△BDE的周长为( )| A、m+n | B、m-n |
| C、2m+n | D、2n+m |
考点:角平分线的性质,等腰直角三角形
专题:
分析:根据角平分线上的点到角的两边距离相等可得CD=DE,然后判断出△ABC和△BDE是等腰直角三角形,根据等腰直角三角形的性质可得BE=DE,再求出DE+BD=BC,从而得解.
解答:解:∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
∴CD=DE,
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AC=BC=m,
又∵DE⊥AB,
∴△BDE是等腰直角三角形,
∴BE=DE=CD=n,
∵DE+BD=CD+BD=BC=AC=m,
∴△BDE的周长=m+n.
故选A.
∴CD=DE,
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AC=BC=m,
又∵DE⊥AB,
∴△BDE是等腰直角三角形,
∴BE=DE=CD=n,
∵DE+BD=CD+BD=BC=AC=m,
∴△BDE的周长=m+n.
故选A.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,等腰直角三角形的判定与性质,熟记各性质是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
 如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )
如图,点O是?ABCD的对角线交点,AC=38mm,BD=24mm,AD=14mm,那么△OBC的周长等于( )| A、40mm | B、44mm |
| C、45mm | D、50mm |
若点A(1,y1)、B(2,y2)都在反比例函数y=
的图象上,则y1,y2的大小关系为( )
| 6 |
| x |
| A、y1≥y2 |
| B、y1>y2 |
| C、y1<y2 |
| D、y1≤y2 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列计算正确的是( )
| A、2a3•3a2=6a6 |
| B、4x3•2x5=8x8 |
| C、2x•2x5=4x5 |
| D、5x3•4x4=9x7 |
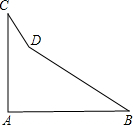 一个零件的形状如图,按要求∠A=90°,∠B=32°,∠C=21°,检验工人量得∠CDB=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.
一个零件的形状如图,按要求∠A=90°,∠B=32°,∠C=21°,检验工人量得∠CDB=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.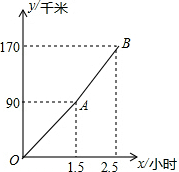 “五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象(OA段和AB段).
“五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象(OA段和AB段).