题目内容
一艘轮船上午6:00从长江上游的A地出发,匀速驶往下游的B地,于11:00到达B地,计划下午13:00从B地匀速返回,如果这段江水流速为3km/h,且轮船在静水中的往返速度不变,那么该船至少以 km/h的速度返回,才能不晚于19:00到达A地.
考点:一元一次不等式的应用
专题:
分析:利用往返路程不变,再结合逆水速度=船的速度-水速以及顺水速度=船的速度+水速得出不等式求出即可.
解答:解:设船xkm/h的速度返回,根据题意得出:
6(x-3)≥5(x+3)
解得:x≥33,
∴该船至少以33km/h的速度返回,才能不晚于19:00到达A地.
故答案为:33.
6(x-3)≥5(x+3)
解得:x≥33,
∴该船至少以33km/h的速度返回,才能不晚于19:00到达A地.
故答案为:33.
点评:此题主要考查了一元一次不等式的应用,根据顺水速以及逆水速度得出不等关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,A、B两点的坐标分别为(-3,5)、(3,5),则点C的坐标为( )
如图,A、B两点的坐标分别为(-3,5)、(3,5),则点C的坐标为( )| A、(1,2) |
| B、(-1,7) |
| C、(3,7) |
| D、(-3,7) |
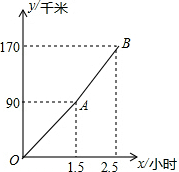 “五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象(OA段和AB段).
“五一节”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象(OA段和AB段). 如图,△ABC的周长是3,以它的三边中点为顶点组成第2个三角形,再以第二个三角形的三边中点为顶点组成的第3个三角形,…,则第n个三角形的周长为
如图,△ABC的周长是3,以它的三边中点为顶点组成第2个三角形,再以第二个三角形的三边中点为顶点组成的第3个三角形,…,则第n个三角形的周长为 如图,将周长为12的△ABC沿BC方向向右平移后得到△DEF,若四边形ABFD的周长为16,则平移的距离是
如图,将周长为12的△ABC沿BC方向向右平移后得到△DEF,若四边形ABFD的周长为16,则平移的距离是 如图,已知AB∥DE,∠ABC=75°,∠CDE=125°,则∠BCD的度数为
如图,已知AB∥DE,∠ABC=75°,∠CDE=125°,则∠BCD的度数为