题目内容
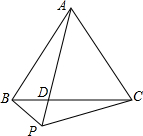 如图所示,点P是等边△ABC外一点,∠APC=60°,PA、BC交于点D,求证:PA=PB+PC.
如图所示,点P是等边△ABC外一点,∠APC=60°,PA、BC交于点D,求证:PA=PB+PC.考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:在AP上截取PE,使得PE=PC,连接CE,得出等边三角形PEC,推出AC=BC,∠ACB=60°,求出∠ACE=∠PCB,证△ACE≌△BCP,推出AE=BP,即可得出答案.
解答:证明:在AP上截取PE,使得PE=PC,连接CE,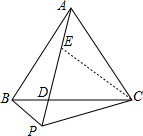
∵∠APC=60°,
∴△PEC是等边三角形
∴PC=CE,∠ECP=60°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠ECP=∠ACB,
∴∠ACE=∠PCB,
在△ACE和△BCP中
,
∴△ACE≌△BCP,
∴AE=BP,
∵AP=AE+PE,
∴AP=PB+PC.

∵∠APC=60°,
∴△PEC是等边三角形
∴PC=CE,∠ECP=60°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠ECP=∠ACB,
∴∠ACE=∠PCB,
在△ACE和△BCP中
|
∴△ACE≌△BCP,
∴AE=BP,
∵AP=AE+PE,
∴AP=PB+PC.
点评:本题考查了等边三角形的性质和判定,全等三角形的性质和判定的应用,题目综合性比较强,难度适中.

练习册系列答案
相关题目
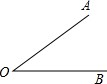 如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由.
如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由. 如图,四边形ABCD内接于⊙O,AB、DC的延长线相交于点E,AD、BC的延长线相交于点F,若∠A=45°,∠E=40°,则∠F=
如图,四边形ABCD内接于⊙O,AB、DC的延长线相交于点E,AD、BC的延长线相交于点F,若∠A=45°,∠E=40°,则∠F=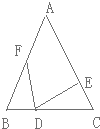 如图,在△ABC中,AB=AC,D为BC上一点,且BD=CE,∠BFD=∠CDE.
如图,在△ABC中,AB=AC,D为BC上一点,且BD=CE,∠BFD=∠CDE.