题目内容
某商场计划购进冰箱、彩电进行销售,相关信息如下表:
(1)若商场用80000元购进冰箱的数量与用64000元购进彩电的数量相等,求表中的a值.
(2)为了满足市场需求,商场决定用不超过90000元的资金采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的
,该商场有那几种进货方式?
(3)在(2)的条件下,若该商场将购进的冰箱、彩电全部售出,获得的利润为y元,请求出y的最大值.
| 进价(元/台) | 售价(元/台) | |
| 冰箱 | a | 2500 |
| 彩电 | a-400 | 2000 |
(2)为了满足市场需求,商场决定用不超过90000元的资金采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的
| 5 |
| 6 |
(3)在(2)的条件下,若该商场将购进的冰箱、彩电全部售出,获得的利润为y元,请求出y的最大值.
考点:一次函数的应用,分式方程的应用,一元一次不等式的应用
专题:
分析:(1)根据彩电和冰箱数量相等列出方程求解即可;
(2)设购进冰箱x台,彩电(50-x)台,然后根据采购资金和冰箱与彩电的数量关系列出不等式组,然后求解,再根据冰箱台数是整数解答;
(3)根据总利润等于每一台的利润乘以台数列式y的表达式,然后根据一次函数的增减性解答.
(2)设购进冰箱x台,彩电(50-x)台,然后根据采购资金和冰箱与彩电的数量关系列出不等式组,然后求解,再根据冰箱台数是整数解答;
(3)根据总利润等于每一台的利润乘以台数列式y的表达式,然后根据一次函数的增减性解答.
解答:解:(1)由题意得,
=
,
解得a=2000,
经检验,a=2000是原分式方程的解;
(2)设购进冰箱x台,则购进彩电(50-x)台,
由题意得,
,
解不等式①得,x≤25,
解不等式②得,x≥
,
所以,
≤x≤25,
∵冰箱台数x是正整数,
∴x取24、25,
所以,商场进货方案为:
方案一:购进24台冰箱,26台彩电,
方案二:购进25台冰箱,25台彩电;
(3)设购进冰箱x台,则购进彩电(50-x)台,
y=(2500-2000)x+(2000-1600)(50-x)=100x+20000,
∵k=100>0,
∴y随x的增大而增大,
∴当购进冰箱25台,彩电25台时,所获利润最大,
最大利润为100×25+20000=22500元.
| 80000 |
| a |
| 64000 |
| a-400 |
解得a=2000,
经检验,a=2000是原分式方程的解;
(2)设购进冰箱x台,则购进彩电(50-x)台,
由题意得,
|
解不等式①得,x≤25,
解不等式②得,x≥
| 250 |
| 11 |
所以,
| 250 |
| 11 |
∵冰箱台数x是正整数,
∴x取24、25,
所以,商场进货方案为:
方案一:购进24台冰箱,26台彩电,
方案二:购进25台冰箱,25台彩电;
(3)设购进冰箱x台,则购进彩电(50-x)台,
y=(2500-2000)x+(2000-1600)(50-x)=100x+20000,
∵k=100>0,
∴y随x的增大而增大,
∴当购进冰箱25台,彩电25台时,所获利润最大,
最大利润为100×25+20000=22500元.
点评:本题考查了一次函数的应用,分式方程的应用,一元一次不等式组的应用,以及利用一次函数的增减性求最值问题,读懂题目信息,找出等量关系和不等量关系是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
去年11月份我市某一天的最高气温是15℃,最低气温是-1℃,那么这一天的最高气温比最低气温高( )
| A、16℃ | B、-15℃ |
| C、14℃ | D、13℃ |
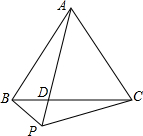 如图所示,点P是等边△ABC外一点,∠APC=60°,PA、BC交于点D,求证:PA=PB+PC.
如图所示,点P是等边△ABC外一点,∠APC=60°,PA、BC交于点D,求证:PA=PB+PC.