题目内容
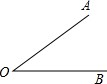 如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由.
如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由.考点:作图—复杂作图,角平分线的性质,线段垂直平分线的性质
专题:
分析:利用线段垂直平分线的性质以及角平分线的性质进而得出Rt△ODP≌Rt△OEP(HL),即可得出答案.
解答: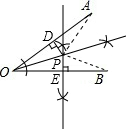 解:如图所示:点P在OA的垂直平分线上,
解:如图所示:点P在OA的垂直平分线上,
理由:过点P作PD⊥OA于点D,
∵∠AOP=∠BOP,
∴PE=PD,
在Rt△ODP和Rt△OEP中
∵
,
∴Rt△ODP≌Rt△OEP(HL),
∴OE=OD,
∵AO=OB,EO=BE,
∴DO=AD,
∴点P在OA的垂直平分线上.
PA=PB,
理由:∵点P在OA的垂直平分线上,点P在OB的垂直平分线上,
∴OP=PA,OP=PB,
∴PA=PB.
 解:如图所示:点P在OA的垂直平分线上,
解:如图所示:点P在OA的垂直平分线上,理由:过点P作PD⊥OA于点D,
∵∠AOP=∠BOP,
∴PE=PD,
在Rt△ODP和Rt△OEP中
∵
|
∴Rt△ODP≌Rt△OEP(HL),
∴OE=OD,
∵AO=OB,EO=BE,
∴DO=AD,
∴点P在OA的垂直平分线上.
PA=PB,
理由:∵点P在OA的垂直平分线上,点P在OB的垂直平分线上,
∴OP=PA,OP=PB,
∴PA=PB.
点评:此题主要考查了复杂作图以及全等三角形的判定与性质、角平分线的性质、线段垂直垂直平分线的性质等知识,熟练应用线段垂直平分线的性质是解题关键.

练习册系列答案
相关题目
 如图,直线y=
如图,直线y=| 1 |
| 3 |
| k |
| x |
| 5 |
| 2 |
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
 如图,AB是⊙O的切线,点B为切点,BC是⊙O的直径,∠A=20°,则∠ODC的度数为( )
如图,AB是⊙O的切线,点B为切点,BC是⊙O的直径,∠A=20°,则∠ODC的度数为( )| A、70° | B、60° |
| C、55° | D、40° |
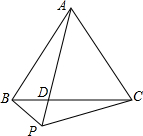 如图所示,点P是等边△ABC外一点,∠APC=60°,PA、BC交于点D,求证:PA=PB+PC.
如图所示,点P是等边△ABC外一点,∠APC=60°,PA、BC交于点D,求证:PA=PB+PC.