题目内容
 如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2.
如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2.求:(1)∠DOM的度数;(2)CD的长.
考点:圆周角定理,垂径定理,圆心角、弧、弦的关系
专题:
分析:(1)根据垂径定理求得
=
,进而求得
=
=
,即可求得∠DOM=
×180°=60°;
(2)连接OC,先求得∠DOM=60°,从而求得∠D=30°,即可求得CD=2CN,根据圆心角、弧、弦的关系求得∠CON=60°,根据圆周角定理求得∠OCN=30°,根据30°的直角三角形的性质即可求得CD的长.
 |
| AD |
 |
| AC |
 |
| AD |
 |
| AC |
 |
| BC |
| 1 |
| 3 |
(2)连接OC,先求得∠DOM=60°,从而求得∠D=30°,即可求得CD=2CN,根据圆心角、弧、弦的关系求得∠CON=60°,根据圆周角定理求得∠OCN=30°,根据30°的直角三角形的性质即可求得CD的长.
解答: 解:(1)∵OA⊥CD于M,
解:(1)∵OA⊥CD于M,
∴
=
,
∵
=
,
∴
=
=
,
∵BD为直径,
∴∠DOM=
×180°=60°;
(2)连接OC,
∵OA⊥CD,∠DOM=60°,
∴∠D=30°,
∴CD=2CN,
∵
=
=
,
∴∠CON=60°,
∴∠OCN=30°,
∵CN⊥DB于N,
∴OC=2ON=4,
∴CN=
=2
,
∴CD=2CN=2×2
=4
.
 解:(1)∵OA⊥CD于M,
解:(1)∵OA⊥CD于M,∴
 |
| AD |
 |
| AC |
∵
 |
| AC |
 |
| BC |
∴
 |
| AD |
 |
| AC |
 |
| BC |
∵BD为直径,
∴∠DOM=
| 1 |
| 3 |
(2)连接OC,
∵OA⊥CD,∠DOM=60°,
∴∠D=30°,
∴CD=2CN,
∵
 |
| AD |
 |
| AC |
 |
| BC |
∴∠CON=60°,
∴∠OCN=30°,
∵CN⊥DB于N,
∴OC=2ON=4,
∴CN=
| OC2-ON2 |
| 3 |
∴CD=2CN=2×2
| 3 |
| 3 |
点评:本题考查了垂径定理,圆心角、弧、弦的关系,圆周角定理等,熟练掌握圆的性质定理是解题的关键.

练习册系列答案
相关题目
将x2-16分解因式正确的是( )
| A、(x-4)2 |
| B、(x-4)(x+4) |
| C、(x+8)(x-8) |
| D、(x-4)2+8x |
如图,在下列四个几何体中,它的三视图(主视图、左视图、俯视图)完全相同的是 ( )


| A、①② | B、②③ | C、①④ | D、②④ |
 如图,在⊙O中,弦AB,AC互相垂直,D,E分别为AB,AC的中点,则四边形OEAD为( )
如图,在⊙O中,弦AB,AC互相垂直,D,E分别为AB,AC的中点,则四边形OEAD为( )| A、正方形 | B、菱形 |
| C、矩形 | D、直角梯形 |
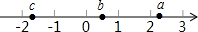 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的有( )
实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的有( )①b+c>0;②a+b>a+c;③bc<ac;④ab>ac.
| A、1个 | B、2个 | C、3个 | D、4个 |
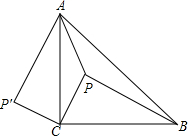 如图,P是等腰Rt△ACB内一点,AC=BC,且PA=8,PB=10,PC=
如图,P是等腰Rt△ACB内一点,AC=BC,且PA=8,PB=10,PC=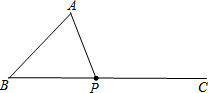 如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP=
如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP=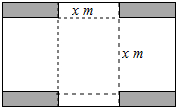 某小区有一块长为40m,宽为30m的长方形空地,现要美化这块空地,在上面修建如图所示的十字形花圃,在花圃内种花,其余部分种草.
某小区有一块长为40m,宽为30m的长方形空地,现要美化这块空地,在上面修建如图所示的十字形花圃,在花圃内种花,其余部分种草.