题目内容
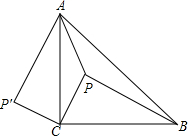 如图,P是等腰Rt△ACB内一点,AC=BC,且PA=8,PB=10,PC=
如图,P是等腰Rt△ACB内一点,AC=BC,且PA=8,PB=10,PC=| 18 |
(1)直接写出旋转的最小角度;
(2)求∠APC的度数.
考点:旋转的性质
专题:计算题
分析:(1)由等腰直角三角形的性质得CA=CB,∠ACB=90°,再根据旋转的性质得∠ACB等于旋转角,于是可判断旋转的最小角度为90°;
(2)连结PP′,如图,根据旋转的性质得∠P′CP=∠ACB=90°,CP′=CP=
,P′A=PB=10,则可判断△CPP′为等腰直角三角形,得到PP′=
CP=6,∠CPP′=45°,然后利用勾股定理的逆定理判断△APP′为直角三角形,∠APP′=90°,于是利用∠APC=∠APP′+∠CPP′计算即可.
(2)连结PP′,如图,根据旋转的性质得∠P′CP=∠ACB=90°,CP′=CP=
| 18 |
| 2 |
解答: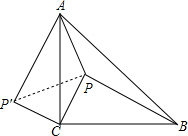 解:(1)∵△ACB为等腰直角三角形,
解:(1)∵△ACB为等腰直角三角形,
∴CA=CB,∠ACB=90°,
∵△CPB绕点C按逆时针方向旋转后,得到△CP′A,
∴∠ACB等于旋转角,
∴旋转的最小角度为90°;
(2)连结PP′,如图,
∵△CPB绕点C按逆时针方向旋转后,得到△CP′A,
∴∠P′CP=∠ACB=90°,CP′=CP=
,P′A=PB=10,
∴△CPP′为等腰直角三角形,
∴PP′=
CP=
×
=6,∠CPP′=45°,
在△APP′中,∵PP′=6,PA=8,P′A=10,
∴PP′2+PA2=P′A2,
∴△APP′为直角三角形,∠APP′=90°,
∴∠APC=∠APP′+∠CPP′=90°+45°=135°.
 解:(1)∵△ACB为等腰直角三角形,
解:(1)∵△ACB为等腰直角三角形,∴CA=CB,∠ACB=90°,
∵△CPB绕点C按逆时针方向旋转后,得到△CP′A,
∴∠ACB等于旋转角,
∴旋转的最小角度为90°;
(2)连结PP′,如图,
∵△CPB绕点C按逆时针方向旋转后,得到△CP′A,
∴∠P′CP=∠ACB=90°,CP′=CP=
| 18 |
∴△CPP′为等腰直角三角形,
∴PP′=
| 2 |
| 2 |
| 18 |
在△APP′中,∵PP′=6,PA=8,P′A=10,
∴PP′2+PA2=P′A2,
∴△APP′为直角三角形,∠APP′=90°,
∴∠APC=∠APP′+∠CPP′=90°+45°=135°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质和勾股定理的逆定理.

练习册系列答案
相关题目
 将图中的△ABC作下列运动,画出相应的图形
将图中的△ABC作下列运动,画出相应的图形 如图,图中已标明了三组互相垂直的线段,那么点B到AC的距离是
如图,图中已标明了三组互相垂直的线段,那么点B到AC的距离是 如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2.
如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2. 如图,在△ABC中,AD为中线,G为重心,且GD=2,则AD=
如图,在△ABC中,AD为中线,G为重心,且GD=2,则AD= 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论: