题目内容
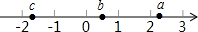实数a、b、c在数轴上的对应点的位置如图所示，下列式子中正确的有（ ）①b+c＞0；②a+b＞a+c；③bc＜ac；④ab＞ac．
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：实数与数轴
专题：
分析：先由数轴可得c＜0＜b＜a，且a＞|c|＞b，再判定即可．
解答：解：∵由数轴可得c＜0＜b＜a，且a＞|c|＞b，
∴①b+c＞0，应为b+c＜0，故不正确；
②a+b＞a+c，正确；
③bc＜ac，应为bc＞ac，故不正确；
④ab＞ac，正确．
共2个正确．
故选：B．
∴①b+c＞0，应为b+c＜0，故不正确；
②a+b＞a+c，正确；
③bc＜ac，应为bc＞ac，故不正确；
④ab＞ac，正确．
共2个正确．
故选：B．
点评：本题主要考查了实数与数轴，解题的关键是利用数轴确定a，b，c的取值范围．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中正确的是（ ）
A、
| ||||
B、函数y=
| ||||
| C、8的立方根是±2 | ||||
| D、点P（2，3）和点Q（2，-3）关于y轴对称 |
如图，C为弧AB中点，OA⊥CD于M，CN⊥DB于N，且BD为直径，ON=2．
如图，点P在线段AB上，点M、N分别是线段AB、AP的中点，若AB=16cm，BP=6cm，求线段NP和线段MN的长．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①因为a＞0，所以函数y有最大值；②该函数的图象关于直线x=-1对称；③a-b+c＞0；④当x=-3或x=1时，函数y的值都等于0．
其中正确结论的个数是（ ）
| A、4 | B、3 | C、2 | D、1 |
如图，如果∠1=∠2=∠3，则AM为△
两圆的半径R，r分别是方程x2-5x+6=0的两根，两圆圆心距为5，则两圆位置关系是（ ）
| A、外离 | B、内含 | C、相交 | D、相切 |
如果|
|=3．|
|=2，且
与
反向，那么下列关系中成立的是（ ）
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|