题目内容
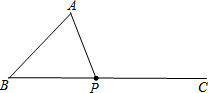 如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP=
如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP=考点:等腰直角三角形
专题:分类讨论
分析:分BP为直角边或斜边来讨论,借助勾股定理逐一解析,即可解决问题.
解答: 解:若BP为三角形的直角边,则AB为该三角形的斜边;
解:若BP为三角形的直角边,则AB为该三角形的斜边;
∵∠B=45°,
∴∠BAP=90°-45°=45°,
∴AP=BP(设为λ);由勾股定理得:
AB2=AP2+BP2=2λ2,而AB=4,
∴λ=
,故答案为
;
若BP为斜边,则∠BAP=90°;
∵∠B=45°,
∴∠APB=90°-45°=45°,
∴∠B=∠APB,
∴AP=AB=4;由勾股定理得:
BP2=AB2+AP2=32,
∴BP=4
(cm).
故答案为4
.
 解:若BP为三角形的直角边,则AB为该三角形的斜边;
解:若BP为三角形的直角边,则AB为该三角形的斜边;∵∠B=45°,
∴∠BAP=90°-45°=45°,
∴AP=BP(设为λ);由勾股定理得:
AB2=AP2+BP2=2λ2,而AB=4,
∴λ=
| 2 |
| 2 |
若BP为斜边,则∠BAP=90°;
∵∠B=45°,
∴∠APB=90°-45°=45°,
∴∠B=∠APB,
∴AP=AB=4;由勾股定理得:
BP2=AB2+AP2=32,
∴BP=4
| 2 |
故答案为4
| 2 |
点评:该题主要考查了等腰三角形的判定、勾股定理等几何知识点的应用问题;借助分类讨论,灵活运用勾股定理等几何知识点来分析、判断、推理活解答是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程是一元一次方程的是( )
| A、x+2y=5 | ||
B、
| ||
| C、2y=1 | ||
| D、x2=8x-3 |
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )| A、15° | B、25° |
| C、10° | D、20° |
 如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2.
如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2. 如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求:
如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求: 如图,点P在线段AB上,点M、N分别是线段AB、AP的中点,若AB=16cm,BP=6cm,求线段NP和线段MN的长.
如图,点P在线段AB上,点M、N分别是线段AB、AP的中点,若AB=16cm,BP=6cm,求线段NP和线段MN的长. 如图,如果∠1=∠2=∠3,则AM为△
如图,如果∠1=∠2=∠3,则AM为△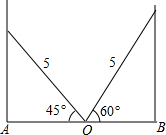 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.
如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为45°,如果梯子的底端O固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为60°,求此保管室的宽度AB的长.