题目内容
某校研究性学习小组在学习完有关交的知识后,利用两个直角∠AOC与∠BOD开展了一下的探究性学习:
(1)如图1,∠AOC=∠BOD=90°,通过观察他们发现∠COD与∠BOA互为补角,请你帮他们说明理由;
(2)分别作∠AOC与∠BOD的平分线OM、ON,得到如图2,他们发现了∠COD与∠MON互为余角,请你帮他们说明理由.
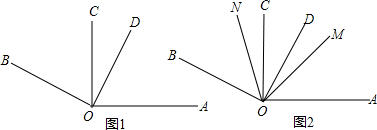
(1)如图1,∠AOC=∠BOD=90°,通过观察他们发现∠COD与∠BOA互为补角,请你帮他们说明理由;
(2)分别作∠AOC与∠BOD的平分线OM、ON,得到如图2,他们发现了∠COD与∠MON互为余角,请你帮他们说明理由.

考点:余角和补角
专题:
分析:(1)反向延长OA到E,即可证得∠BOE=∠COD,据此即可求解;
(2)首先求得∠AOM和∠BON的度数,则∠MON=∠AOB-∠AOM-∠BON=∠AOB-90°,然后根据(1)的结论即可求解.
(2)首先求得∠AOM和∠BON的度数,则∠MON=∠AOB-∠AOM-∠BON=∠AOB-90°,然后根据(1)的结论即可求解.
解答: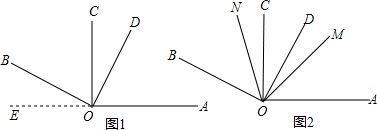 解:(1)∵反向延长OA到E.
解:(1)∵反向延长OA到E.
∵∠AOC=90°,
∴∠COE=90°,
又∵∠BOD=90°,
∴∠BOE+∠BOC=∠BOC+∠COD=90°,
∴∠BOE=∠COD,
∴∠COD+∠BOA=180°,即∠COD与∠BOA互为补角;
(2)∵OM、ON分别是∠AOC与∠BOD的角平分线,
∴∠AOM=
∠AOC=45°,∠BON=
∠BOD=45°,
∴∠MON=∠AOB-∠AOM-∠BON=∠AOB-90°,
又∵∠COD+∠BOA=180°,
∴∠COD+∠MON=90°.
 解:(1)∵反向延长OA到E.
解:(1)∵反向延长OA到E.∵∠AOC=90°,
∴∠COE=90°,
又∵∠BOD=90°,
∴∠BOE+∠BOC=∠BOC+∠COD=90°,
∴∠BOE=∠COD,
∴∠COD+∠BOA=180°,即∠COD与∠BOA互为补角;
(2)∵OM、ON分别是∠AOC与∠BOD的角平分线,
∴∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠AOB-∠AOM-∠BON=∠AOB-90°,
又∵∠COD+∠BOA=180°,
∴∠COD+∠MON=90°.
点评:本题考查了补角和余角的定义,利用∠AOB表示出∠MON是本题的关键.

练习册系列答案
相关题目
下列说法中正确的是( )
A、
| ||||
B、函数y=
| ||||
| C、8的立方根是±2 | ||||
| D、点P(2,3)和点Q(2,-3)关于y轴对称 |
 将图中的△ABC作下列运动,画出相应的图形
将图中的△ABC作下列运动,画出相应的图形 如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2.
如图,C为弧AB中点,OA⊥CD于M,CN⊥DB于N,且BD为直径,ON=2.