题目内容
9.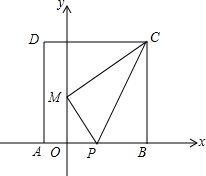 将正方形ABCD放置在如图所示的直角坐标系中,点B的坐标为(8,0),点P在边AB的中点.连结CP,将△BCP沿PC折叠,使点B落在y轴的M点处,且点M的纵坐标为4.若点Q是x轴正半轴上一个运动的点,连结MQ、CQ,则△CMQ周长的最小值为10+2$\sqrt{65}$.
将正方形ABCD放置在如图所示的直角坐标系中,点B的坐标为(8,0),点P在边AB的中点.连结CP,将△BCP沿PC折叠,使点B落在y轴的M点处,且点M的纵坐标为4.若点Q是x轴正半轴上一个运动的点,连结MQ、CQ,则△CMQ周长的最小值为10+2$\sqrt{65}$.
分析 作点M关于x轴的对称点M′,连接CM′与x轴的交点即为点Q,此时△CMQ周长最小,先在RT△OMP中利用勾股定理求出OP,正方形边长,然后在RT△CNM′利用勾股定理求出CM′即可解决问题.
解答 解: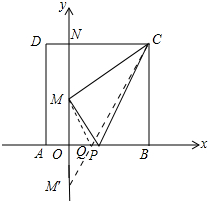 作点M关于x轴的对称点M′,连接CM′与x轴的交点即为点Q,此时△CMQ周长最小,
作点M关于x轴的对称点M′,连接CM′与x轴的交点即为点Q,此时△CMQ周长最小,
设OP=x,则PB=PM=8-x,
在RT△OPM中,PM2=OM2+OP2,
∴(8-x)2=42+x2,
∴x=3,
∴PM=PB=5,AB=2PB=BC=10,
设CD与y轴交于点N,
在RT△CNM′中,∠CNM′=90°,CN=8,NM′=14,
∴CM′=$\sqrt{C{N}^{2}+NM{′}^{2}}$=$\sqrt{{8}^{2}+1{4}^{2}}$=2$\sqrt{65}$,
∴△CMQ的周长=CM+CQ+MQ=CM+CQ+QM′=CM+CM′=10+2$\sqrt{65}$.
点评 本题考查正方形的性质、轴对称-最短问题、勾股定理等知识,解题的关键是利用勾股定理求出正方形的边长,学会利用轴对称解决最短问题,属于中考常考题型.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
16.不等式1≤$\frac{x-2}{3}$<5的解集是( )
| A. | 3≤x≤15 | B. | 5≤x<13 | C. | 5≤x<17 | D. | -3≤x<15 |
1.已知关于x的方程x2-kx-4=0的一个根为x=3,则实数k的值为( )
| A. | 5 | B. | 3 | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
19.若关于x的一元二次方程x2-(a+5)x+8a=0的两个实数根分别为2和b,则ab=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.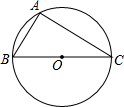 如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.
如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.