题目内容
14．
某种商品每天的销售利润y（元）与销售单价x（元）之间满足关系：y=ax2+bx-75，其图象如图所示．（1）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？
（2）销售单价在什么范围时，该商品每天的销售利润不低于16元？
（3）若点A关于原点的对称点为点C，求△OBC的面积．
分析 （1）根据待定系数法，可得二次函数解析式，根据顶点坐标，可得答案；
（2）根据函数值大于或等于16，可得不等式的解集，可得答案；
（3）根据题意求出点B、点C的坐标，再根据面积公式计算即可．
解答 解：（1）将点A（7，16）、（5，0）代入y=ax2+bx-75，
得：$\left\{\begin{array}{l}{49a+7b-75=16}\\{25a+5b-75=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-1}\\{b=20}\end{array}\right.$，
故抛物线解析式为：y=-x2+20x-75=-（x-10）2+25，
当x=10是，y取得最大值25，
答：销售单价为10元时，该种商品每天的销售利润最大，最大利润为25元；
（2）∵函数y=-x2+20x-75图象的对称轴为直线x=10，
可知点（7，16）关于对称轴的对称点是（13，16），
又∵函数y=-x2+20x-75图象开口向下，
∴当7≤x≤13时，y≥16．
答：销售单价不少于7元且不超过13元时，该种商品每天的销售利润不低于16元；
（3）点A（7，16）关于原点的对称点为点C坐标为（-7，-16），
在y=-x2+20x-75中，当y=0时有-x2+20x-75=0，
解得：x=5或x=15，
∴点B坐标为（15，0），
故S△OBC=$\frac{1}{2}$×15×16=120．
点评 本题考查了待定系数求二次函数解析式、二次函数的图象与性质及三角形面积求法，熟练掌握二次函数的图象与性质是关键．
练习册系列答案
名校课堂系列答案
相关题目
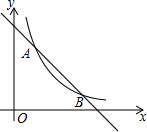如图，一次函数y=kx+b（k、b为常数，且k≠0）的图象与反比例函数y=$\frac{3}{x}$的图象交于A（1，a），B（3，1）两点．
如图，AB、CD相交于点O，EO⊥DC，∠AOE的余角是∠AOD，∠COB的补角是∠AOC和∠BOD．
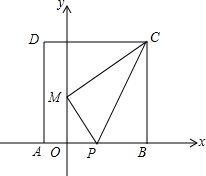将正方形ABCD放置在如图所示的直角坐标系中，点B的坐标为（8，0），点P在边AB的中点．连结CP，将△BCP沿PC折叠，使点B落在y轴的M点处，且点M的纵坐标为4．若点Q是x轴正半轴上一个运动的点，连结MQ、CQ，则△CMQ周长的最小值为10+2$\sqrt{65}$．
如图，已知AD∥BC，∠1=∠2，说明BE∥DF的理由．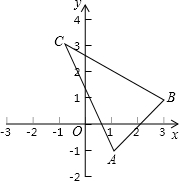
如图，△ABC在平面直角坐标系中，点A（1，-1），点B（3，1），点C（-1，3），将△ABC绕点O旋转90°后得△A1，B1，C1，求点A1，B1，C1的坐标．