题目内容
 如图,每个小正方形的边长均为1,求四边形ABCD的面积和周长(精确到0.1).
如图,每个小正方形的边长均为1,求四边形ABCD的面积和周长(精确到0.1).考点:勾股定理,三角形的面积
专题:网格型
分析:首先根据勾股定理求得AB、BC、CD、DA、AC的长,根据勾股定理的逆定理判断∠ABC和∠ACD是直角,即可求解.
解答:解:根据勾股定理得到:AD=
=5
;AB=
=2
;CD=
=5;BC=
=
.
AC=
=5.

∴四边形ABCD的周长是:AB+BC+CD+AD=5
+2
+
+5=5
+3
+5;
∵(2
)2+(
)2=52,52+52=(5
)2.
∴BC2+AB2=AC2,AC2+CD2=AD2.
∴∠ABC和∠ACD是直角.
∴四边形ABCD的面积=直角△ABC的面积+直角△ACD的面积=
BC•AB+
AC•CD=17.5.
故四边形ABCD的面积是17.5,周长是5
+3
+5.
| 72+12 |
| 2 |
| 22+42 |
| 5 |
| 32+42 |
| 12+22 |
| 5 |
AC=
| 42+32 |

∴四边形ABCD的周长是:AB+BC+CD+AD=5
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
∵(2
| 5 |
| 5 |
| 2 |
∴BC2+AB2=AC2,AC2+CD2=AD2.
∴∠ABC和∠ACD是直角.
∴四边形ABCD的面积=直角△ABC的面积+直角△ACD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故四边形ABCD的面积是17.5,周长是5
| 2 |
| 5 |
点评:本题主要考查运用勾股定理和勾股定理的逆定理,正确判断∠ABC和∠ACD是直角是解决本题的关键.

练习册系列答案
相关题目
来自某综合市场财务部的报告表明,商场2014年1-4月份的投资总额一共是2017万元,商场2014年第一季度每月利润统计图和2014年1-4月份利润率统计图如下(利润率=利润÷投资金额):

根据以上信息,下列判断不正确的是( )

根据以上信息,下列判断不正确的是( )
| A、商场2014年第一季度中3月份投资金额最多 |
| B、商场2014年第一季度中2月份投资金额最少 |
| C、商场2014年4月份利润比2月份的利润高 |
| D、商场四个月的利润所组成的一组数据的中位数是124 |
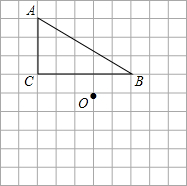 如图,已知一个直角三角形ABC和点O在网格中.
如图,已知一个直角三角形ABC和点O在网格中. 完成下面的证明过程.
完成下面的证明过程. 全民健身是指不分男女老少,全面提高国民体质和健康水平,以青少年和儿童为重点,每年进行一次体质测定.小明和爷爷二人同时从家到健身馆,小明跑步,爷爷步行,小明到达健身馆后休息了5分钟,然后以练习竞走的方式迎接爷爷,速度为原来的一半,在途中与爷爷相遇,二人之间的距离y(m)与时间x(分)之间的关系如图,则小明家到健身馆的距离为
全民健身是指不分男女老少,全面提高国民体质和健康水平,以青少年和儿童为重点,每年进行一次体质测定.小明和爷爷二人同时从家到健身馆,小明跑步,爷爷步行,小明到达健身馆后休息了5分钟,然后以练习竞走的方式迎接爷爷,速度为原来的一半,在途中与爷爷相遇,二人之间的距离y(m)与时间x(分)之间的关系如图,则小明家到健身馆的距离为