题目内容
某纪念币从2013年11月11日起开始上市,通过市场调查得知该纪念币每1枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
(1)根据上表数据,从下列函数中选取一个恰当的函数描述纪念币的市场价y与上市时间x的变化关系:
①y=ax+b;②y=ax2+bx+c;③y=
.
你选择的函数序号是 ,理由是 .
(2)利用你选取的函数,求该纪念币市场价最低时的上市天数及最低的价格.
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
①y=ax+b;②y=ax2+bx+c;③y=
| a |
| x |
你选择的函数序号是
(2)利用你选取的函数,求该纪念币市场价最低时的上市天数及最低的价格.
考点:二次函数的应用
专题:
分析:(1)根据表格中数据变化规律可得出答案;
(2)利用待定系数法求二次函数解析式,进而利用最值求法得出答案.
(2)利用待定系数法求二次函数解析式,进而利用最值求法得出答案.
解答:解:(1)根据题意得出:y与上市时间x的变化关系是②;
理由:随时间x的增加,y的值先减后增;
(2)把点(4,90),(10,51),(36,90)代入y=ax2+bx+c中,得:
,
解得:
,
∴y=
x2-10x+126=
(x-20)2+26,
当x=20,y有最小值,y最小=26,
答:纪念品市场价最低时的上市天数为20天,最低按价格为26元.
理由:随时间x的增加,y的值先减后增;
(2)把点(4,90),(10,51),(36,90)代入y=ax2+bx+c中,得:
|
解得:
|
∴y=
| 1 |
| 4 |
| 1 |
| 4 |
当x=20,y有最小值,y最小=26,
答:纪念品市场价最低时的上市天数为20天,最低按价格为26元.
点评:此题主要考查了待定系数法求二次函数解析式以及配方法求二次函数最值,正确得出二次函数解析式是解题关键.

练习册系列答案
相关题目
 如图,每个小正方形的边长均为1,求四边形ABCD的面积和周长(精确到0.1).
如图,每个小正方形的边长均为1,求四边形ABCD的面积和周长(精确到0.1).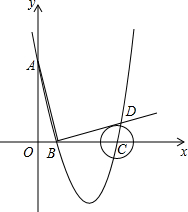 如图,在平面直角坐标系中,顶点为(3,-4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,5).
如图,在平面直角坐标系中,顶点为(3,-4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,5).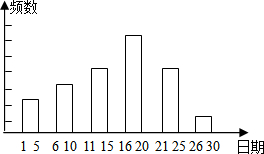 某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:
某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答: 已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且
已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且 如图,点B在点A北偏东50°方向,点C在点B北偏西40°方向,BC=10m,则点C到直线AB的距离为
如图,点B在点A北偏东50°方向,点C在点B北偏西40°方向,BC=10m,则点C到直线AB的距离为