题目内容
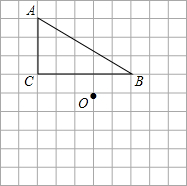如图，已知一个直角三角形ABC和点O在网格中．（1）作△ABC关于点O对称的△A′B′C′；
（2）用直尺和圆规作△ABC的∠B和∠C的平分线，并标出两条角平分线的交点P；指出点P是△ABC的内心还是△ABC的外心？（要求：保留作图痕迹，不必写作法和证明）
考点：作图-旋转变换,三角形的外接圆与外心,三角形的内切圆与内心
专题：
分析：（1）根据题意得出A，B，C关于O点对称点，进而得出△A′B′C′；
（2）利用三角形角平分线的作法以及三角形内心的定义得出即可．
（2）利用三角形角平分线的作法以及三角形内心的定义得出即可．
解答：
解：（1）如图所示：△A′B′C′即为所求；
（2）如图所示：P点即为所求，P点是△ABC的外心．
解：（1）如图所示：△A′B′C′即为所求；（2）如图所示：P点即为所求，P点是△ABC的外心．
点评：此题主要考查了旋转变换以及三角形内心的作法，正确得出变换后对应点位置是解题关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
如图，点A、B、C为⊙O上的三点，连接AC，若∠OCA=40°，则∠ABC的度数为下列说法正确的是（ ）
A、
| ||
B、
| ||
| C、3x是整式 | ||
| D、x的系数为0 |
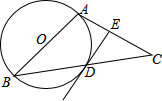如图，在等腰△ABC中，AB=AC，以AB为直径作⊙O交底边BC于D．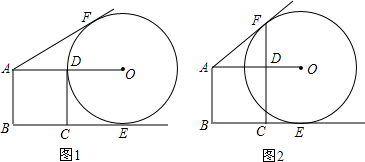
如图，每个小正方形的边长均为1，求四边形ABCD的面积和周长（精确到0.1）．
已知：在平面直角坐标系中，点A、B的坐标分别是（a，0），（b，0）且