题目内容
7.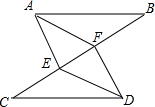 如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )
如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )| A. | ∠B=∠C | B. | AF=FD | C. | AE=DF | D. | AB∥DC |
分析 因为AB=DC,AE=DF,BF=CE,可证明△AEB≌△DFC,再对选项一一分析,采用排除法选择正确答案.
解答 解:∵BF=CE,
∴BF+EF=CE+EF
即BE=CF
在△AEB和△DFC中,
$\left\{\begin{array}{l}{BE=CF}\\{AB=DC}\\{AE=DF}\end{array}\right.$
∴△AEB≌△DFC,
∴AE=DF,故C成立;
∠B=∠C,故A成立;
∴∠B=∠C,
∴AB∥DC,故D成立;
在△ABF和△CDE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{BF=CE}\end{array}\right.$
∴△ABF≌△CDE,
∴AF=DE,故B成立;
故选:B.
点评 此题把全等三角形的判定和平行线的判定结合起来,解决本题的关键是证明△ABF≌△CDE.

练习册系列答案
相关题目
2.直线y=kx+3过点(-2,0),则k的值是( )
| A. | -2 | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -3 |
17.下列说法正确的是( )
| A. | -0.064的立方根是0.4 | |
| B. | 一个数的平方根与它的立方根相等,则这个数是0 | |
| C. | -9的平方根是±3 | |
| D. | -7是(-7)2的算术平方根 |
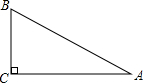 如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.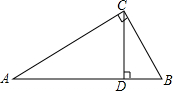 如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,DB=1cm.求:
如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,DB=1cm.求: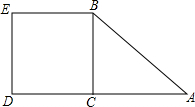 如图,已知Rt△ABC中,∠ACB=90°,AB=10cm,AC=8cm,则正方形BCDE的面积是36cm2.
如图,已知Rt△ABC中,∠ACB=90°,AB=10cm,AC=8cm,则正方形BCDE的面积是36cm2.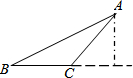 如图,△ABC中,∠B=30°,∠A=15°,若BC边上的高为2,则BC=2$\sqrt{3}$-2.
如图,△ABC中,∠B=30°,∠A=15°,若BC边上的高为2,则BC=2$\sqrt{3}$-2.