题目内容
15.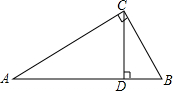 如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,DB=1cm.求:
如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,DB=1cm.求:(1)CD和AC的长;
(2)求AB的长.
分析 (1)由△ABC中∠ACB=90°,∠A=30°,得到∠B=60°,由于DC⊥AB,得到∠CDB=90°,于是得到∠DCB=30°,求得BC=2cm,AB=4cm,根据勾股定理即可得到结论;
(2)根据直角三角形的性质有一个角等于30度,那么它所对的直角边等于斜边的一半即可得到结果.
解答 解:(1)∵△ABC中∠ACB=90°,∠A=30°,
∴∠B=60°,
∵DC⊥AB,
∴∠CDB=90°,
∴∠DCB=30°,
∴BD=$\frac{1}{2}$BC=1cm,
∴BC=2cm,AB=4cm,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{3}$,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{3}$;
(2)∵△ABC中∠ACB=90°,∠A=30°,
∴AB=2BC=4cm.
点评 本题考查了含30度角的直角三角形性质的应用,注意:在直角三角形中,如果有一个角等于30度,那么它所对的直角边等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.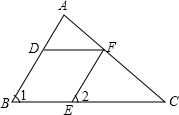 如图,点D、E、F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( )
如图,点D、E、F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( )
 如图,点D、E、F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( )
如图,点D、E、F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件( )| A. | ∠1=∠2 | B. | ∠1=∠DFE | C. | ∠1=∠AFD | D. | ∠2=∠AFD |
20.在实数:5.2,-$\frac{2}{3}$,0.028,$\sqrt{3}$,$\root{3}{10}$,3$\frac{1}{2}$,3.14中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.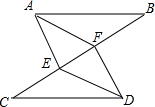 如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )
如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )
 如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )
如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )| A. | ∠B=∠C | B. | AF=FD | C. | AE=DF | D. | AB∥DC |
4.下列说法正确的是( )
| A. | 对角线相等且互相垂直的四边形是菱形 | |
| B. | 对角线互相垂直的平行四边形是正方形 | |
| C. | 对角线相等且互相平分的四边形是矩形 | |
| D. | 对角线互相垂直的菱形是正方形 |



