题目内容
10．已知二次函数y=ax2+bx+c与自变量x的部分对应值如表：| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
①该函数开口向下．
②该函数图象的对称轴为过点（1，0）且平行于y轴的直线．
③当x=2时，y=3．
④方程ax2+bx+c=-2的正根在3与4之间．
其中正确的说法为①③④．（只需写出序号）
分析 利用表中函数值的变换情况可判断抛物线的开口方向，则可对①进行判断；利用x=0和x=3时函数值相等可得到抛物线的对称轴方程，则可对②进行判断；利用抛物线的对称性可得x=1和x=2的函数值相等，则可对③进行判断；利用抛物线的对称性可得x=-1和x=4的函数值相等，则可对④进行判断．
解答 解：∵二次函数值先由小变大，再由大变小，
∴抛物线的开口向下，所以①正确；
∵抛物线过点（0，1）和（3，1），
∴抛物线的对称轴为直线x=$\frac{3}{2}$，所以②错误；
点（1，3）和点（2，3）为对称点，所以③正确；
∵x=-1时，y=-3，
∴x=4时，y=-3，
∴二次函数y=ax2+bx+c的函数值为-2时，-1＜x＜0或3＜x＜4，
即方程ax2+bx+c=-2的负根在-1与0之间，正根在3与4之间，所以④正确．
故答案为①③④．
点评 本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），对称轴直线x=-$\frac{b}{2a}$．熟练掌握二次函数的性质和抛物线的对称性是解决此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．已知关于x的方程ax2+bx+c=5的一个根是2，且二次函数y=ax2+bx+c的对称轴是直线x=2，则这条抛物线的顶点坐标为（ ）
| A． | （2，-3） | B． | （2，1） | C． | （2，5） | D． | （5，2） |
1．在平面直角坐标系中，若y轴上的点P到x轴的距离为3，则点P的坐标为（ ）
| A． | （3，0） | B． | （3，0）或（-3，0） | C． | （0，3） | D． | （0，3）或（0，-3） |
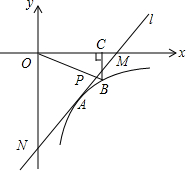如图，在平面直角坐标系中，直线l与坐标轴相交于点M（3，0），N（0，-4），反比例函数y=$\frac{k}{x}$（x＞0）的图象经过Rt△MON的外心A．