已知关于x的方程ax2+bx+c=5的一个根是2.且二次函数y=ax2+bx+c的对称轴是直线x=2.则这条抛物线的顶点坐标为( )A．B．(2.1)C．(2.5)D．(5.2) 题目和参考答案——青夏教育精英家教网—

题目内容

20．已知关于x的方程ax²+bx+c=5的一个根是2，且二次函数y=ax²+bx+c的对称轴是直线x=2，则这条抛物线的顶点坐标为（　　）

A．

（2，-3）

B．

（2，1）

C．

（2，5）

D．

（5，2）

分析由二次函数y=ax²+bx+c的对称轴是直线x=2，得出顶点横坐标为2，代入函数解析式得出纵坐标ax²+bx+c=5，由此求得顶点坐标即可．

解答解：∵二次函数y=ax²+bx+c的对称轴是直线x=2，方程ax²+bx+c=5的一个根是2，
∴当x=2时，y=ax²+bx+c=5，
∴抛物线的顶点坐标是（2，5）．
故选：C．

点评本题考查的是二次函数的性质，掌握顶点坐标的计算方法是解决问题的关键．

练习册系列答案

相关题目

20．

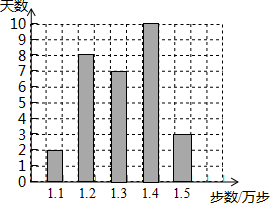赵老师是一名健步走运动的爱好者，她用手机软件记录了某个月（30天）每天健步走的步数（单位：万步），将记录结果绘制成了如图所示的统计图．在每天所走的步数这组数据中，众数和中位数分别是（　　）

11．下面4个图均由6个小正方形组成，若以每个小正方形为面，则可以折叠成正方体的是（　　）

8．把下列各数填在相应的位置：-5，+$\frac{1}{5}$，0.64，0，-1.1，$\frac{6}{7}$，8，|-10|，-（-5）
（1）分数：+$\frac{1}{5}$，0.64，-1.1，$\frac{6}{7}$
（2）整数：-5，0，8，|-10|，-（-5）
（3）非负数：+$\frac{1}{5}$，0.64，0，$\frac{6}{7}$，8，|-10|，-（-5）．

15．8²⁰¹⁶×0.125²⁰¹⁵=8．

5．把函数y=-2x的图象向下平移1个单位，所得图象的函数解析式为（　　）

12．点A（9-a，a-3）在第一、三象限的角平分线上，则点A的坐标为（3，3）．

9．

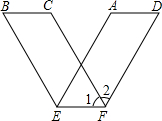用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案，已知图中∠1=62°，则∠2的度数为56°．

10．已知二次函数y=ax²+bx+c与自变量x的部分对应值如表：

x	…	-1	0	1	3	…
y	…	-3	1	3	1	…

现给出下列说法：
①该函数开口向下．
②该函数图象的对称轴为过点（1，0）且平行于y轴的直线．
③当x=2时，y=3．
④方程ax²+bx+c=-2的正根在3与4之间．
其中正确的说法为①③④．（只需写出序号）

试题分类