题目内容
2.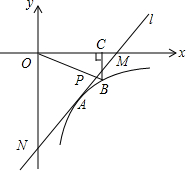 如图,在平面直角坐标系中,直线l与坐标轴相交于点M(3,0),N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过Rt△MON的外心A.
如图,在平面直角坐标系中,直线l与坐标轴相交于点M(3,0),N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过Rt△MON的外心A.(1)求直线l的解析式;
(2)直接写出点A坐标及k值;
(3)在函数y=$\frac{k}{x}$(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△OMP的面积与△OBC的面积相等,求点P的坐标.
分析 (1)设直线l的解析式为y=kx+b,把M(3,0),N(0,-4)代入,即可求出k、b,即可得出答案;
(2)求出A为MN的中点,即可得出答案;
(3)设P点的坐标为(a,$\frac{4}{3}$a-4),分别表示出两个三角形的面积,即可得出方程,求出a的值,即可得出答案.
解答 解:(1)设直线l的解析式为y=kx+b,
把M(3,0),N(0,-4)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=-4}\end{array}\right.$,
解得:k=$\frac{4}{3}$,b=-4,
所以直线l的解析式为y=$\frac{4}{3}$x-4;
(2)∵点A是直角三角形NOM的外心,
∴A为MN的中点,
∵M(3,0),N(0,-4),
∴A的坐标为($\frac{3}{2}$,-2),
把A的坐标代入y=$\frac{k}{x}$得:k=-3;
(3)∵点P在直线l上,且在第四象限,可设P点的坐标为(a,$\frac{4}{3}$a-4),
∴S△OMP=$\frac{1}{2}×3×|\frac{4}{3}a-4|$=$\frac{1}{2}$×3×(4-$\frac{4}{3}$a),
∵点B是y=-$\frac{3}{x}$上的点,
∴S△OBC=$\frac{1}{2}$•|k|=$\frac{3}{2}$,
∵△OMP的面积与△OBC的面积相等,
∴$\frac{1}{2}$×3×(4-$\frac{4}{3}$a)=$\frac{3}{2}$,
解得:a=$\frac{9}{4}$,
∴$\frac{4}{3}$a-4=$\frac{4}{3}$×$\frac{9}{4}$-4=-1,
∴P的坐标为($\frac{9}{4}$,-1).
点评 本题考查了用待定系数法求一次函数和反比例函数的解析式,三角形的面积,三角形的外接圆的应用,能用待定系数法求出函数的解析式是解此题的关键.

 阅读快车系列答案
阅读快车系列答案| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
①该函数开口向下.
②该函数图象的对称轴为过点(1,0)且平行于y轴的直线.
③当x=2时,y=3.
④方程ax2+bx+c=-2的正根在3与4之间.
其中正确的说法为①③④.(只需写出序号)
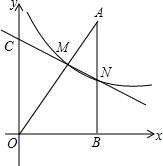 如图,在平面直角坐标系中,A点的坐标是(3,4),AB⊥x轴于点B,反比例函数y=$\frac{k}{x}$的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.
如图,在平面直角坐标系中,A点的坐标是(3,4),AB⊥x轴于点B,反比例函数y=$\frac{k}{x}$的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM. 如图,正方形ABCD的边BC在y轴上,点D的坐标为(2,3),反比例函数y=$\frac{k}{x}$的图象经过点A,交边CD于点N,过点M(t,0),作直线EM垂直于x轴,交双曲线于点E,交直线AB于点F.
如图,正方形ABCD的边BC在y轴上,点D的坐标为(2,3),反比例函数y=$\frac{k}{x}$的图象经过点A,交边CD于点N,过点M(t,0),作直线EM垂直于x轴,交双曲线于点E,交直线AB于点F. 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,AB=2$\sqrt{2}$.
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,AB=2$\sqrt{2}$.