题目内容
8.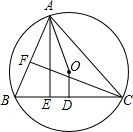 如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).
如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).
分析 连接BO,CO,根据圆周角定理得到∠BOD=$\frac{1}{2}∠$BOC=∠BAC=60°,求得∠AOB=∠AOD-∠BOD=105°,根据吹径定理得到OD⊥BC,求得AE∥OD,根据平行线的性质得到∠OAE=180°-∠AOD=15°,即可得到结论.
解答  解:连接BO,CO,
解:连接BO,CO,
∵∠A=60°
∴∠BOD=$\frac{1}{2}∠$BOC=∠BAC=60°,
∵∠AOD=165°,
∴∠AOB=∠AOD-∠BOD=105°,∠BAO=$\frac{1}{2}$(180°-∠AOB)=37.5°,
∵AE⊥BC,OD⊥BC,
∴AE∥OD,
∴∠OAE=180°-∠AOD=15°,
∴∠BAE=∠BAO-∠OAE=22.5°.
点评 本题考查了圆周角定理,平行线的判定和性质,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
16.某果品公司要请汽车运输公司或火车货运站将60吨水果从A地运到B地.已知汽车和火车从A地到B地的运输路程都是x千米,两家运输单位除都要收取运输途中每吨每小时5元的冷藏费外,其他要收取的费用和有关运输资料由下表列出:
(1)用含x的式子分别表示汽车货运公司和火车货运站运送这批水果所要收取的总费用(总运费=运费+运输途中冷藏费+装卸总费用);
(2)果品公司应该选择哪家运输单位运送水果花费少?
| 运输单位 | 运输速度 (千米/时) | 运费单价 元/(吨•千米) | 运输途中冷藏 元/(吨•时) | 装卸总费用(元) |
| 汽车货运公司 | 75 | 1.5 | 5 | 4000 |
| 火车货运站 | 100 | 1.3 | 5 | 6600 |
(2)果品公司应该选择哪家运输单位运送水果花费少?
20.若一次函数y=kx+b的图象经过第一、二、三象限,则k、b的取值范围是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
 如图.在△ABC中,点D在BC边上,BD=DC,点E在AD上,CF∥AB,∠BAD=∠DEF,若AB=5,CF=2.则线段EF的长为3.
如图.在△ABC中,点D在BC边上,BD=DC,点E在AD上,CF∥AB,∠BAD=∠DEF,若AB=5,CF=2.则线段EF的长为3.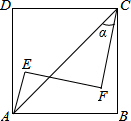 如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.
如图,正方形ABCD内有两点E、F满足AE=4,tanα=$\frac{3}{4}$,AE⊥EF,CF⊥EF,EF=CF,则正方形的边长为10$\sqrt{2}$.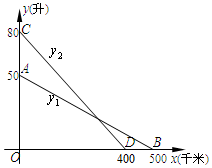 如图,线段AB、CD分别是一辆轿车的油箱剩余油量y1(升)与另一辆客车的油箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.
如图,线段AB、CD分别是一辆轿车的油箱剩余油量y1(升)与另一辆客车的油箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.