题目内容
18.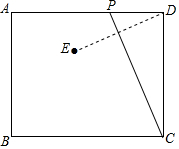 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
分析 (1)如图1中,设PD=t.则PA=6-t.首先证明BP=BC=6,在Rt△ABP中利用勾股定理即可解决问题;
(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3;
解答 解:(1)如图1中,设PD=t.则PA=6-t.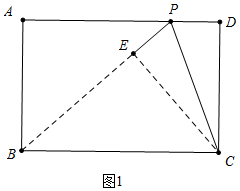
∵P、B、E共线,
∴∠BPC=∠DPC,
∵AD∥BC,
∴∠DPC=∠PCB,
∴∠BPC=∠PCB,
∴BP=BC=6,
在Rt△ABP中,∵AB2+AP2=PB2,
∴42+(6-t)2=62,
∴t=6-2$\sqrt{5}$或6+2$\sqrt{5}$(舍弃),
∴PD=6-2$\sqrt{5}$,
∴t=(6-2$\sqrt{5}$)s时,B、E、P共线.
(2)如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90°,
∴EM=$\sqrt{E{C}^{2}-C{M}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
$\frac{AD}{DM}$=$\frac{DC}{EM}$,
∴$\frac{AD}{7}$=$\frac{4}{\sqrt{7}}$,
∴AD=4$\sqrt{7}$,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
在Rt△ECQ中,QC=DM=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
由△DME∽△CDA,
∴$\frac{DM}{CD}$=$\frac{EM}{AD}$,
∴$\frac{\sqrt{7}}{4}$=$\frac{1}{AD}$,
∴AD=$\frac{4\sqrt{7}}{7}$,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围$\frac{4\sqrt{7}}{7}$≤m<4$\sqrt{7}$.
点评 本题考查四边形综合题、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会利用特殊位置解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| 月份n(月) | 1 | 2 |
| 成本y(万元/件) | 11 | 12 |
| 需求量x(件/月) | 120 | 100 |
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
| A. | $\sqrt{8}$=2$\sqrt{2}$ | B. | 面积是8的正方形的边长是$\sqrt{8}$ | ||
| C. | $\sqrt{8}$是有理数 | D. | 在数轴上可以找到表示$\sqrt{8}$的点 |
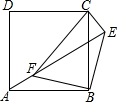 如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.
如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.
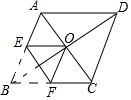 如图,菱形ABCD的对角线相交于点O,AC=2,BD=2$\sqrt{3}$,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为7.
如图,菱形ABCD的对角线相交于点O,AC=2,BD=2$\sqrt{3}$,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为7.