题目内容
8.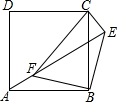 如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.
如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.(1)求证:△ABF≌△CBE;
(2)填空:用等式表示线段FA、FE、FC之间的数量关系为FE2=FA2+FC2.
分析 (1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;
(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB=135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形,再根据勾股定理即可证明;
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABF=∠CBE}\\{BF=BE}\end{array}\right.$,
∴△ABF≌△CBE(SAS).
(2)解:结论:FE2=FA2+FC2.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形,
∵FE2=FC2+EC2,
∵△ABF≌△CBE,
∴AF=EC,
∴FE2=FA2+FC2.
故答案为FE2=FA2+FC2.
点评 本题考查了正方形的性质.全等三角形的判定及性质、等腰直角三角形的性质以及角的计算,解题的关键是:(1)根据判定定理SAS证明△ABF≌△CBE;(2)通过角的计算得出∠CEF=90°.本题属于中档题,难度不大,解决该题型题目时,通过正方形和等腰三角形的性质找出相等的边,再通过角的计算找出相等的角,以此来证明两三角形全等是关键.

| A. | 1 | B. | -1 | C. | 4 | D. | $-\frac{1}{4}$ |
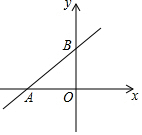 如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )
如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )| A. | x>-3 | B. | x<-3 | C. | x>2 | D. | x<2 |
| A. |  | B. |  | C. |  | D. |  |
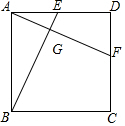 如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.
如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.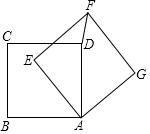 如图,正方形AEFG与正方形ABCD的边长都为2,正方形AEFG绕正方形ABCD的顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值可以为1或2或3或4.
如图,正方形AEFG与正方形ABCD的边长都为2,正方形AEFG绕正方形ABCD的顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值可以为1或2或3或4.
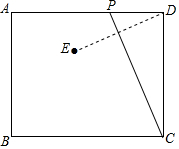 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).