题目内容
8．解方程 （用适当方法）（1）3（x-1）2=48；
（2）2x（x-3）=（x-3）．
分析 （1）直接开平方法求解可得；
（2）因式分解法求解可得．
解答 解：（1）∵（x-1）2=16，
∴x-1=4或x-1=-4，
解得：x=5或x=-3；
（2）∵2x（x-3）-（x-3）=0，
∴（x-3）（2x-1）=0，
则x-3=0或2x-1=0，
解得：x=3或x=0.5．
点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键
练习册系列答案
相关题目
19．
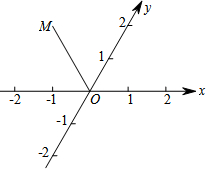在平面上，过一定点O作两条斜交的轴x和y，它们的交角是ω（ω≠90°），以定点O为原点，在每条轴上取相同的单位长度，这样就在平面上建立了一个斜角坐标系，其中ω叫做坐标角．对于平面内任意一点P，过P作x轴和y轴的平行线，与两轴分别交于A和B，它们在两轴的坐标分别是x和y，于是点P的坐标就是（x，y）．如图，ω=60°，且y轴平分∠MOx，OM=2，则点M的坐标是（ ）
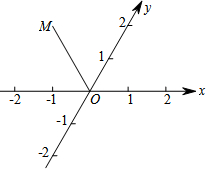在平面上，过一定点O作两条斜交的轴x和y，它们的交角是ω（ω≠90°），以定点O为原点，在每条轴上取相同的单位长度，这样就在平面上建立了一个斜角坐标系，其中ω叫做坐标角．对于平面内任意一点P，过P作x轴和y轴的平行线，与两轴分别交于A和B，它们在两轴的坐标分别是x和y，于是点P的坐标就是（x，y）．如图，ω=60°，且y轴平分∠MOx，OM=2，则点M的坐标是（ ）| A． | （2，-2） | B． | （-1，2） | C． | （-2，2） | D． | （-2，1） |
16．下列说法中，正确的是（ ）
| A． | 对角线相等的四边形是矩形 | |
| B． | 对角线互相平分的四边形是平行四边形 | |
| C． | 对角线平分一组对角的四边形是菱形 | |
| D． | 对角线互相垂直的四边形是菱形 |
17．
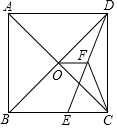如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若△CEF的周长为18，则OF的长为（ ）
如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若△CEF的周长为18，则OF的长为（ ）| A． | 3 | B． | 4 | C． | $\frac{5}{2}$ | D． | $\frac{7}{2}$ |
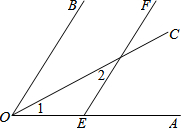如图，OC是∠AOB的平分线，且∠1=∠2，探索EF与OB的位置关系，并说明理由．