题目内容
18.为迎接G20杭州峰会的召开,某校八年级(1)(2)班准备集体购买一种T恤衫参加一项社会活动.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.如果八(1)(2)班共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买数量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,则第一批T恤衫的购买40件.分析 设第一批购买x件,则第二批购买(100-x)件,分两种情况:①当30<x≤40时,则60≤100-x<100;②当40<x<60时,则40<100-x<60;根据购买两批T恤衫一共花了9200元列出方程求解即可.
解答 解:设第一批购买x件,则第二批购买(100-x)件.
①$\left\{\begin{array}{l}{30<x≤40}\\{x(150-x)+80(100-x)=9200}\end{array}\right.$,
解得x1=30(舍去),x2=40;
②$\left\{\begin{array}{l}{40<x<60}\\{x(150-x)+(100-x)[150-(100-x)]=9200}\end{array}\right.$
无实数解;
所以:第一批购买数量为40件.
故答案是:40.
点评 考查了一元一次不等式组的应用,根据实际问题列一次函数关系式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
18.若分式$\frac{1}{x+3}$的值大于0,则实数x的取值范围是( )
| A. | x>-3 | B. | x≥-3 | C. | x>3 | D. | x≠-3 |
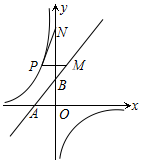 在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.
在平面直角坐标系中,已知点A(-$\sqrt{2}$,0)、B(0,$\sqrt{2}$)、N(0,3$\sqrt{2}$),P是反比例函数y=-$\frac{1}{x}$(x<0)的图象上一动点,PM∥x轴交直线AB于M,则PM+PN的最小值为$\frac{7\sqrt{2}}{3}$.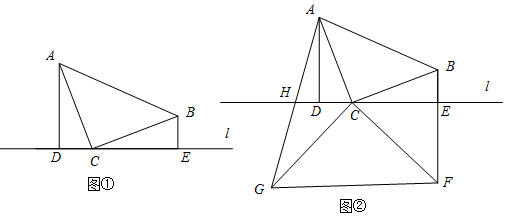
 如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.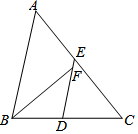 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是1.
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是1.