题目内容
17.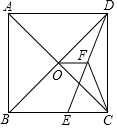 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )| A. | 3 | B. | 4 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
分析 先根据直角三角形的性质求出DE的长,再由勾股定理得出CD的长,进而可得出BE的长,由三角形中位线定理即可得出结论.
解答 解:∵CE=5,△CEF的周长为18,
∴CF+EF=18-5=13.
∵F为DE的中点,
∴DF=EF.
∵∠BCD=90°,
∴CF=$\frac{1}{2}$DE,
∴EF=CF=$\frac{1}{2}$DE=6.5,
∴DE=2EF=13,
∴CD=$\sqrt{D{E}^{2}-C{E}^{2}}=\sqrt{1{3}^{2}-{5}^{2}}=12$.
∵四边形ABCD是正方形,
∴BC=CD=12,O为BD的中点,
∴OF是△BDE的中位线,
∴OF=$\frac{1}{2}$(BC-CE)=$\frac{1}{2}$(12-5)=$\frac{7}{2}$.
故选D
点评 本题考查的是正方形的性质,涉及到直角三角形的性质、三角形中位线定理等知识,难度适中.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
7.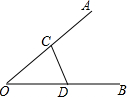 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )| A. | 线段CD的中点 | B. | CD与∠AOB平分线的交点 | ||
| C. | OC垂直平分线与CD的交点 | D. | OD垂直平分线与CD的交点 |
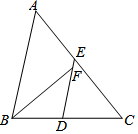 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是1.
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是1.
 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交干A、B两点,与x轴、y轴分别交于C、D两点,与x轴、y轴分别交于C,D两点,若CD=2$\sqrt{5}$,tan∠ACO=$\frac{1}{2}$,点A的坐标为(m,3).
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交干A、B两点,与x轴、y轴分别交于C、D两点,与x轴、y轴分别交于C,D两点,若CD=2$\sqrt{5}$,tan∠ACO=$\frac{1}{2}$,点A的坐标为(m,3). 如图所示,A、B的坐标分别为(2,0),(0,1),AB∥A1B1,AB=A1B1,则a-b的值是( )
如图所示,A、B的坐标分别为(2,0),(0,1),AB∥A1B1,AB=A1B1,则a-b的值是( )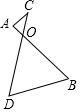 如图,AB=CD,AB与DC相交于点O,∠AOC=60°,请你利用平移的有关知识说明:AC+BD>AB.
如图,AB=CD,AB与DC相交于点O,∠AOC=60°,请你利用平移的有关知识说明:AC+BD>AB.