题目内容

14．求不等式组$\left\{\begin{array}{l}2x＜x+1\\ \frac{2-x}{3}≤2\end{array}\right.$的整数解．

分析 分别求出不等式组中两不等式的解集，找出解集的公共部分确定出不等式组的解集，即可确定出整数解．

解答 解：$\left\{\begin{array}{l}{2x＜x+1①}\\{\frac{2-x}{3}≤2②}\end{array}\right.$，
解不等式①，得x＜1，
解不等式②，得x≥-4，
在同一数轴上表示不等式①②的解集，如图

∴原不等式组的解集为-4≤x＜1，
则原不等式组的整数解为-4，-3，-2，-1，0．

点评 此题考查了一元一次不等式的整数解，求出不等式组的解集是解本题的关键．

练习册系列答案
相关题目
4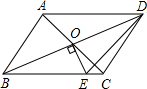．如图，平行四边形ABCD的对角线相交于点O，且DC≠AD，过点O作OE⊥BD交BC于点E，若△CDE的周长为6cm，则平行四边形ABCD的周长为（　　）
A．6cmB．8cmC．10cmD．12cm
5．某公司2012年缴税70万元，2014年缴税90万元，求该公司这两年缴税的年平均增长率．若设该公司这两年缴税的年平均增长率为x，根据题意，可得方程（　　）
A．70x2=90B．70（1+x）2=90
C．70（1+x）=90D．70+70（1+x）+70（1+x）2=90
2．如果若有理数a和b在数轴上所表示的点分别在原点的右边和左边，则$\sqrt{b^2}$-|a-b|=-a．
9．解不等式组$\left\{\begin{array}{l}{x-2＞0①}\\{-2x+6≥0②}\end{array}\right.$
请结合题意填空，完成本题的解答：
（Ⅰ）解不等式①，得x＞2；
（Ⅱ）解不等式②，得x≤3；
（Ⅲ）把不等式①和②的解集在数轴上表示出来：

（Ⅳ）原不等式组的解集为2＜x≤3．
19．先化简，再求值：（2a+b）（2a-b）-$\frac{1}{2}$a（8a-2ab），其中a=-$\frac{1}{2}$，b=2．
6．若关于m的不等式的解集如图所示，则关于x的不式（m-3）x＜3-m的解集为x＞-1．
3．设x1，x2是方程2x2-$\sqrt{6}$x-1=0的两根，不解方程，求下列各式的值．
（1）${x}_{1}^{2}$+${x}_{2}^{2}$；（2）（x1-x2）2．
4．不等式组$\left\{\begin{array}{l}{x+1＞0}\\{x-3＞0}\end{array}\right.$的解集是（　　）
A．x＞-1B．x＞3C．-1＜x＜3D．x＜3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网