题目内容
3.设x1,x2是方程2x2-$\sqrt{6}$x-1=0的两根,不解方程,求下列各式的值.(1)${x}_{1}^{2}$+${x}_{2}^{2}$;(2)(x1-x2)2.
分析 根据根与系数的关系得出“x1+x2=-$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$,x1•x2=$\frac{c}{a}$=-$\frac{1}{2}$”.
(1)利用完全平方公式,将${{x}_{1}}^{2}+{{x}_{2}}^{2}$转化成$({x}_{1}+{x}_{2})^{2}$-2x1•x2,代入数据即可得出结论;
(2)利用完全平方公式,将$({x}_{1}-{x}_{2})^{2}$转化成$({x}_{1}+{x}_{2})^{2}$-4x1•x2,代入数据即可得出结论.
解答 解:∵x1,x2是方程2x2-$\sqrt{6}$x-1=0的两根,
∴x1+x2=-$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$,x1•x2=$\frac{c}{a}$=-$\frac{1}{2}$.
(1)${{x}_{1}}^{2}+{{x}_{2}}^{2}$=$({x}_{1}+{x}_{2})^{2}$-2x1•x2=$(\frac{\sqrt{6}}{2})^{2}$-2×(-$\frac{1}{2}$)=$\frac{5}{2}$;
(2)$({x}_{1}-{x}_{2})^{2}$=$({x}_{1}+{x}_{2})^{2}$-4x1•x2=$(\frac{\sqrt{6}}{2})^{2}$-4×(-$\frac{1}{2}$)=$\frac{7}{2}$.
点评 本题考查了根与系数的关系以及完全平方公式,解题的关键是:(1)将原代数式转化成$({x}_{1}+{x}_{2})^{2}$-2x1•x2;(2)将原代数式转化成$({x}_{1}+{x}_{2})^{2}$-4x1•x2.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积,再利用完全平方公式将原代数式转化成只含两根之和与两根之积的代数式是关键.

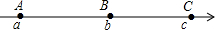 如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,则下列关系正确的是( )
如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,则下列关系正确的是( )| A. | a+c=2b | B. | b>c | C. | c-a=2(a-b) | D. | a=c |
 由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.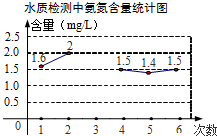 为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是1mg/L.
为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是1mg/L.