题目内容
10．一个三角形的两边长分别为2和6，则第三边的长可能为（ ）| A． | 4 | B． | 7 | C． | 8 | D． | 10 |
分析 根据三角形三边关系：任意两边之和大于第三边以及任意两边之差小于第三边，即可得出第三边的取值范围，然后从答案中选取即可．
解答 解：∵此三角形的两边长分别为2和6，
∴第三边长的取值范围是：6-2=4＜第三边＜6+2=8．
即：4＜x＜8，7符合要求，
故选B．
点评 此题主要考查了三角形三边关系，根据第三边的范围是：大于已知的两边的差，而小于两边的和是解决问题的关键．
练习册系列答案
春雨教育同步作文系列答案
相关题目
1．
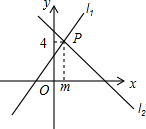如图l1：y=x+3与l2：y=ax+b相交于点P（m，4），则关于x的不等式x+3≤ax+b的解为（ ）
如图l1：y=x+3与l2：y=ax+b相交于点P（m，4），则关于x的不等式x+3≤ax+b的解为（ ）| A． | x≥4 | B． | x＜m | C． | x≥m | D． | x≤1 |
5．若一次函数y=（m-3）x+（m+1）（其中m为常数）的图形经过第一、二、四象限，则m的取值范围是（ ）
| A． | -1≤m≤3 | B． | m＜3 | C． | -1＜m＜3 | D． | m＞3 |
15．下列二次根式中，是最简二次根式的是（ ）
| A． | $\sqrt{15}$ | B． | $\sqrt{12}$ | C． | $\sqrt{\frac{1}{3}}$ | D． | $\sqrt{9}$ |