题目内容
20.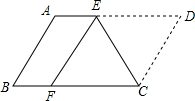 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,则四边形ABFE的周长为12.
分析 (1)根据折叠的性质得到EF=ED,∠CFE=∠CDE,根据平行四边形的性质得到AD∥BC,∠B=∠D,由平行线的判定得到AE∥BF,即可得到结论;
(2)根据平行四边形的性质得到EF=AB=4.求得ED=4,得到AE=BF=6-4=2,于是得到结论.
解答 (1)证明:∵将 ABCD沿CE折叠,使点D落在BC边上的F处,
∴EF=ED,∠CFE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴AE∥BF,∠B=∠CFE,
∴AB∥EF,
∴四边形ABFE为平行四边形;
(2):∵四边形ABFE为平行四边形,
∴EF=AB=4,
∵EF=ED,
∴ED=4,
∴AE=BF=6-4=2,
∴四边形ABFE的周长=AB+BF+EF+EA=12,
故答案为:12
点评 本题考查了平行四边形的判定和性质,折叠的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )
如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )
 如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )
如图,将矩形纸片ABCD沿CE向上折叠,使点B落在AD边上的点F处,若AE=$\frac{1}{2}$BE,则$\frac{CD}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
8.已知P1(-1,y1),P2(2,y2)是一次函数y=-x+1图象上的两个点,则y1,y2的大小关系是( )
| A. | y1=y2 | B. | y1<y2 | C. | y1>y2 | D. | 不能确定 |
15. 如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.
如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.
 如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.
如图,在等腰直角△ABC中,∠C=90°,AD是∠CAB的平分线,DE⊥AB,且DE=2cm,则AE的长是( )cm.| A. | 2$\sqrt{2}$+2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 不确定 |
5.若一次函数y=(m-3)x+(m+1)(其中m为常数)的图形经过第一、二、四象限,则m的取值范围是( )
| A. | -1≤m≤3 | B. | m<3 | C. | -1<m<3 | D. | m>3 |
1.若m<n,则下列各式正确的是( )
| A. | $\frac{m}{2}$>$\frac{n}{2}$ | B. | m-2<n-2 | C. | -3m<-3n | D. | -a2m<-a2n |