题目内容
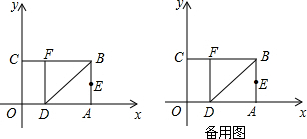
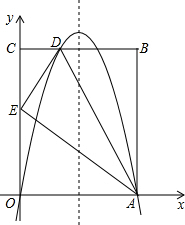
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且EF=PF,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且EF=PF,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.

考点:二次函数综合题
专题:
分析:(1)E为AB中点,则横坐标、纵坐标分别为3,1,故坐标为(3,1);由A落在F处,则BF=AB=3,所以横坐标、纵坐标分别为1,2,故坐标为(1,2).
(2)因为FP=EF且图中并无已知位置,所以画圆是找全所有情况的最好办法,发现y轴上存在两点P,使得FP=EF,进一步根据三角形性质可得到坐标,但要考虑题目中对P点的要求对最后结果进行取舍.求抛物线解析式通常采用的方法为待定系数法,注意题中已知F为顶点,故利用顶点式设抛物线解析式求解过程会简单很多.
(3)四边形周长最小我们基本没有接触过,但是周长中其中EF固定,那么周长最小就转化为三段折现最短,恰起止两点已经固定,这是我们在学对称轴时常见的画图找最短路径题目,即利用两次对称点性质将问题转化为两个点间路径最短的问题,则N、M两点易找到,进而最短周长易求.
(2)因为FP=EF且图中并无已知位置,所以画圆是找全所有情况的最好办法,发现y轴上存在两点P,使得FP=EF,进一步根据三角形性质可得到坐标,但要考虑题目中对P点的要求对最后结果进行取舍.求抛物线解析式通常采用的方法为待定系数法,注意题中已知F为顶点,故利用顶点式设抛物线解析式求解过程会简单很多.
(3)四边形周长最小我们基本没有接触过,但是周长中其中EF固定,那么周长最小就转化为三段折现最短,恰起止两点已经固定,这是我们在学对称轴时常见的画图找最短路径题目,即利用两次对称点性质将问题转化为两个点间路径最短的问题,则N、M两点易找到,进而最短周长易求.
解答:解:
(1)E(3,1),F(1,2).
(2)
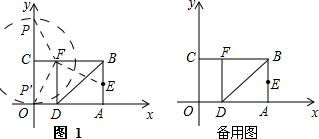
如图1,以点C为圆心,BF为半径画弧交y轴于P,P',连接EF,FP,FP'.
∵CF⊥PP',CP=CP'
∴F在PP'的垂直平分线上,
∴FP=FP'.
在△FCP和△EBF中,
,
∴△FCP≌△EBF,
∴FP=EF,CP=BF,
∴FP=FP'=EF,CP=CP'=BF=2,
∴P(0,4),P'(0,0)(此点不在y的正半轴上,舍去),
∵F(1,2)为抛物线顶点,
∴设抛物线解析式y=a(x-1)2+2,
∴代入P(0,4),解得a=2,y=2(x-1)2+2=2x2-4x+4.
(3)
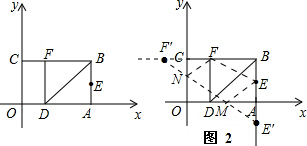
如图2,作E点关于x轴的对称的E',做F点关于y轴的对称的F',连接E'F'交x轴,y轴分别为M,N,连接EF,EM,FM.
∵NF=NF',EM=E'M,
∴C四边形NMEF=FM+NM+ME+FE=NF'+NM+ME'+EF=E'F'+EF,
根据两点间线段最短得,此时C四边形NMEF最小.
∵E(3,1),F(1,2),
∴E'(3,-1),F(-1,2),
∴BF'=4,BE'=3,
∴根据勾股定理,E'F'=5,
∵EF=
,
∴当C四边形NMEF最小时,C四边形NMEF=E'F'+EF=5+
.
(1)E(3,1),F(1,2).
(2)

如图1,以点C为圆心,BF为半径画弧交y轴于P,P',连接EF,FP,FP'.
∵CF⊥PP',CP=CP'
∴F在PP'的垂直平分线上,
∴FP=FP'.
在△FCP和△EBF中,
|
∴△FCP≌△EBF,
∴FP=EF,CP=BF,
∴FP=FP'=EF,CP=CP'=BF=2,
∴P(0,4),P'(0,0)(此点不在y的正半轴上,舍去),
∵F(1,2)为抛物线顶点,
∴设抛物线解析式y=a(x-1)2+2,
∴代入P(0,4),解得a=2,y=2(x-1)2+2=2x2-4x+4.
(3)

如图2,作E点关于x轴的对称的E',做F点关于y轴的对称的F',连接E'F'交x轴,y轴分别为M,N,连接EF,EM,FM.
∵NF=NF',EM=E'M,
∴C四边形NMEF=FM+NM+ME+FE=NF'+NM+ME'+EF=E'F'+EF,
根据两点间线段最短得,此时C四边形NMEF最小.
∵E(3,1),F(1,2),
∴E'(3,-1),F(-1,2),
∴BF'=4,BE'=3,
∴根据勾股定理,E'F'=5,
∵EF=
| 5 |
∴当C四边形NMEF最小时,C四边形NMEF=E'F'+EF=5+
| 5 |
点评:本题考查了三角形性质,待定系数求抛物线解析式及路径最短等基础知识,数据不复杂,难度也适中,是一道非常值得学生巩固练习的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在直角坐标系中,A点在x轴上,AB∥y轴,C点在y轴上,CB∥x轴,点B的坐标为(8,10),点D在BC上,将△ABD沿直线AD翻折,使得点B刚好落在y轴的点E处.
如图,在直角坐标系中,A点在x轴上,AB∥y轴,C点在y轴上,CB∥x轴,点B的坐标为(8,10),点D在BC上,将△ABD沿直线AD翻折,使得点B刚好落在y轴的点E处.