题目内容
解关于x的分式方程:
-
-
=2(a+b≠0).
| a+b |
| x |
| b |
| a |
| a |
| b |
考点:解分式方程
专题:计算题
分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:去分母得:ab(a+b)-b2x-a2x=2abx,
移项合并得:(a2+b2+2ab)x=ab(a+b),即(a+b)2x=ab(a+b),
∵a+b≠0,
∴x=
,
经检验是分式方程的解.
移项合并得:(a2+b2+2ab)x=ab(a+b),即(a+b)2x=ab(a+b),
∵a+b≠0,
∴x=
| ab |
| a+b |
经检验是分式方程的解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
如果点P(-5,y)在第三象限,则y的取值范围是( )
| A、y<0 |
| B、y>0 |
| C、y大于或等于0 |
| D、y小于或等于0 |
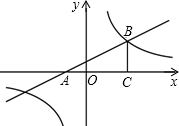 如图,平面直角坐标系中,直线
如图,平面直角坐标系中,直线
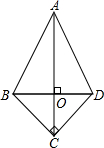 如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=
如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=