题目内容
△ABC的底边BC=8cm,当BC边上的高线从小到大变化时,△ABC的面积也随之变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)△ABC的面积y(cm2)与高线x(cm)的关系式是什么?
(3)用表格表示当x由5cm变到15cm时(每次增加2),y的相应值;
(4)当x每增加2cm时,y如何变化?
(1)在这个变化过程中,自变量和因变量各是什么?
(2)△ABC的面积y(cm2)与高线x(cm)的关系式是什么?
(3)用表格表示当x由5cm变到15cm时(每次增加2),y的相应值;
(4)当x每增加2cm时,y如何变化?
考点:函数关系式,常量与变量,函数值
专题:
分析:(1)△ABC的面积也随高线的变化而变化,因而高线是自变量,△ABC的面积是因变量.
(2)根据三角形的面积公式就可以得到.
(3)已知x的几个值就可以求出相应的函数值.得到图表.
(4)根据图表就可以得到当x每增加2cm时,y的变化.
(2)根据三角形的面积公式就可以得到.
(3)已知x的几个值就可以求出相应的函数值.得到图表.
(4)根据图表就可以得到当x每增加2cm时,y的变化.
解答:解:(1)在这个变化过程中,BC边上的高线AD是自变量,△ABC的面积是因变量.
(2)y=
•BC•x=
×8•x=4x,即y与x之间的关系式是y=4x.
(3)列表格如下:
(4)由(3)可看出,当x每增加1cm时,y增加8cm2.
(2)y=
| 1 |
| 2 |
| 1 |
| 2 |
(3)列表格如下:
| x(cm) | 5 | 7 | 9 | 11 | 13 | 15 | … |
| y(cm2) | 20 | 28 | 36 | 44 | 42 | 60 | … |
点评:此题主要考查了列函数关系式,利用三角形的面积公式S=
ah,可找出问题的突破口,体会高与面积之间的变化关系.
| 1 |
| 2 |

练习册系列答案
相关题目
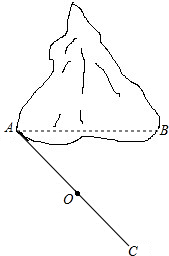 如图,山脚下有A、B两点,用两种方法测量A、B两点间的距离.
如图,山脚下有A、B两点,用两种方法测量A、B两点间的距离.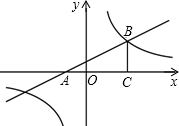 如图,平面直角坐标系中,直线
如图,平面直角坐标系中,直线 已知,如图,在△ABC中,∠A=90°,DE为BC的垂直平分线,求证:BE2=AC2+AE2.
已知,如图,在△ABC中,∠A=90°,DE为BC的垂直平分线,求证:BE2=AC2+AE2.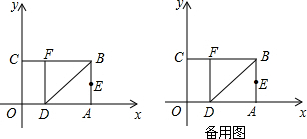
 如图:已知四边形ABCD是平行四边形,DE⊥AB于点E,点M为BC的中点,BC=2AB,∠BEM=50°,求∠B的度数.
如图:已知四边形ABCD是平行四边形,DE⊥AB于点E,点M为BC的中点,BC=2AB,∠BEM=50°,求∠B的度数. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至20℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系.
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至20℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系.