题目内容
同一平面内的两条直线有相交和平行两种位置关系.
(1)如图a,若AB∥CD,点P在AB、CD外部,我们过点P作AB、CD的平行线PE,则有AB∥CD∥PE,故∠B=∠BPE,∠D=∠DPE,故∠BPE=∠BPD+∠DPE,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,利用(1)中的结论(可以直接套用)求∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?
(3)设BF交AC于点P,AE交DF于点Q.已知∠APB=130°,∠AQF=110°,利用(2)的结论直接写出∠B+∠E+∠F的度数为 度,∠A比∠F大 度.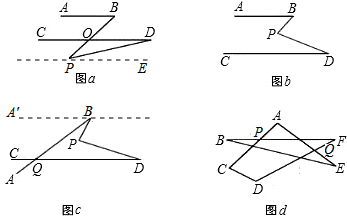
(1)如图a,若AB∥CD,点P在AB、CD外部,我们过点P作AB、CD的平行线PE,则有AB∥CD∥PE,故∠B=∠BPE,∠D=∠DPE,故∠BPE=∠BPD+∠DPE,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,利用(1)中的结论(可以直接套用)求∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?
(3)设BF交AC于点P,AE交DF于点Q.已知∠APB=130°,∠AQF=110°,利用(2)的结论直接写出∠B+∠E+∠F的度数为

考点:平行线的性质
专题:
分析:(1)依据两直线平行内错角相等,三角形外角的性质即可求得.
(2)依据两直线平行内错角相等,三角形外角的性质即可求得.
(3)依据(2)中的结论、三角形的内角和及三角形的外角和即可求得.
(2)依据两直线平行内错角相等,三角形外角的性质即可求得.
(3)依据(2)中的结论、三角形的内角和及三角形的外角和即可求得.
解答:(1)∠BPD=∠B-∠D不成立,是∠BPD=∠B+∠D,
证明:如图b,延长BP交DC于M,
∵AB∥CD,
∴∠B=∠BMD,
∵∠BPD=∠BMD+∠D,
∴∠BPD=∠B+∠D;
(2)∠BPD=∠B+∠D+∠BQD;
∵A′B∥CD,
∴∠A′BQ=∠BQD,
证明同(1).
(3)解∵∠AQF=110°,
∴∠EQF=∠B+∠E+∠F=180°-110°=70°,
∵∠1=∠APB-∠A=130°-∠A,∠2=180°-∠AQF-∠F=180°-110°-∠F=70°-∠F;
∵∠1=∠2,
∴130°-∠A=70°-∠F;
∴∠A-∠F=60°.

证明:如图b,延长BP交DC于M,
∵AB∥CD,
∴∠B=∠BMD,
∵∠BPD=∠BMD+∠D,
∴∠BPD=∠B+∠D;
(2)∠BPD=∠B+∠D+∠BQD;
∵A′B∥CD,
∴∠A′BQ=∠BQD,
证明同(1).
(3)解∵∠AQF=110°,
∴∠EQF=∠B+∠E+∠F=180°-110°=70°,
∵∠1=∠APB-∠A=130°-∠A,∠2=180°-∠AQF-∠F=180°-110°-∠F=70°-∠F;
∵∠1=∠2,
∴130°-∠A=70°-∠F;
∴∠A-∠F=60°.
点评:本题考查了平行线性质,三角形外角性质,四边形的内角和定理等知识点的应用,主要考查学生的推理能力和猜想能力.

练习册系列答案
相关题目
 如图:已知四边形ABCD是平行四边形,DE⊥AB于点E,点M为BC的中点,BC=2AB,∠BEM=50°,求∠B的度数.
如图:已知四边形ABCD是平行四边形,DE⊥AB于点E,点M为BC的中点,BC=2AB,∠BEM=50°,求∠B的度数. 已知如图的坐标系中两直线l1和l2,求这两条直线的交点坐标.
已知如图的坐标系中两直线l1和l2,求这两条直线的交点坐标.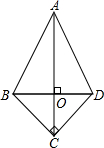 如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=
如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=